Calculer les charges, contraintes, déformations
Comprendre les charges, contraintes et déformations
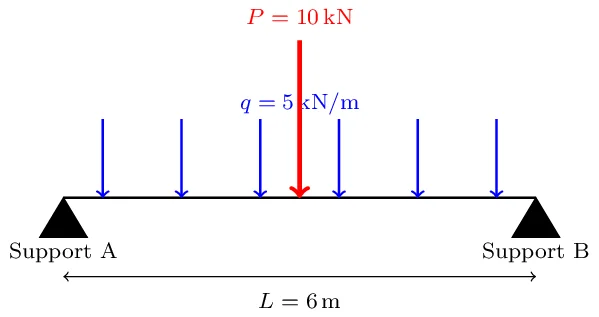
Une poutre en acier simplement appuyée aux deux extrémités. Cette poutre est soumise à une charge uniformément répartie (charge distribuée) ainsi qu’à une charge ponctuelle située au milieu de sa longueur.
Pour comprendre le Calcul des déformations dans une poutre, cliquez sur le lien.
Données
- Longueur de la poutre, \( L \): 6 mètres.
- Module d’élasticité de l’acier, \( E \): 200 GPa (GigaPascals).
- Moment d’inertie de la section de la poutre, \( I \): \( 4 \times 10^{-6} \, \text{m}^4 \).
- Charge uniformément répartie, \( q \): 5 kN/m (kiloNewtons par mètre).
- Charge ponctuelle, \( P \): 10 kN (kiloNewtons), appliquée au milieu de la poutre.
Questions:
1. Calculer la réaction aux appuis.
2. Déterminer la position et la valeur de la contrainte maximale dans la poutre.
3. Calculer la déformation maximale de la poutre.
Remarques
- Considérez que la poutre est dans un régime élastique linéaire, c’est-à-dire que la loi de Hooke est applicable.
- Les calculs doivent tenir compte des unités correctes et de leur conversion si nécessaire.
Correction : les charges, contraintes et déformations
1. Calcul des réactions aux appuis
Pour une poutre simplement appuyée, l’équilibre statique (somme des forces verticales et des moments) permet de déterminer les réactions aux appuis. Ici, la poutre est soumise :
- À une charge uniformément répartie \(q\) sur toute la longueur \(L\);
- À une charge ponctuelle \(P\) appliquée au milieu de la poutre.
Les réactions seront symétriques, car la charge totale et leur répartition sont symétriques.
Formules
- Sommation des forces verticales :
\[ R_A + R_B = qL + P \]
- Moment autour d’un appui (par exemple, A) :
\[ R_B \times L = qL \times \frac{L}{2} + P \times \frac{L}{2} \]
d’où,
\[ R_B = \frac{qL \times \frac{L}{2} + P \times \frac{L}{2}}{L} = \frac{qL + P}{2} \]
Données
- \(L = 6\,\text{m}\)
- \(q = 5\,\text{kN/m}\)
- \(P = 10\,\text{kN}\)
Calcul
1. Calcul de la charge totale:
\[ qL + P = 5\,\text{kN/m} \times 6\,\text{m} + 10\,\text{kN} \] \[ qL + P = 30\,\text{kN} + 10\,\text{kN} \] \[ qL + P = 40\,\text{kN} \]
2. Réaction à \(B\) (ou \(A\)):
\[ R_B = \frac{40\,\text{kN}}{2} = 20\,\text{kN} \]
3. Par équilibre vertical:
\[ R_A = 40\,\text{kN} – 20\,\text{kN} \] \[ R_A = 20\,\text{kN} \]
Conclusion :
Les réactions aux appuis sont :
\[ R_A = R_B = 20\,\text{kN} \]
2. Détermination de la contrainte maximale (flexion)
La contrainte de flexion dans une poutre est donnée par la formule :
\[ \sigma = \frac{M\,c}{I} \]
où :
- \(M\) est le moment fléchissant,
- \(c\) est la distance entre le neutre et la fibre la plus éloignée (la “cote” de la section),
- \(I\) est le moment d’inertie de la section.
Pour une charge combinée, le moment fléchissant maximum se trouve au milieu de la poutre et est la somme des contributions de :
- La charge uniformément répartie : \(M_{\text{udl}} = \frac{qL^2}{8}\)
- La charge ponctuelle appliquée en milieu de poutre : \(M_{\text{point}} = \frac{P L}{4}\)
Formules
- Moment dû à la charge uniformément répartie :
\[ M_{\text{udl}} = \frac{qL^2}{8} \]
- Moment dû à la charge ponctuelle :
\[ M_{\text{point}} = \frac{P L}{4} \]
- Moment fléchissant total :
\[ M_{\max} = M_{\text{udl}} + M_{\text{point}} \]
- Contrainte maximale en flexion :
\[ \sigma_{\max} = \frac{M_{\max}\,c}{I} \]
Données
- \(L = 6\,\text{m}\)
- \(q = 5\,\text{kN/m}\)
- \(P = 10\,\text{kN}\)
- \(I = 4 \times 10^{-6}\,\text{m}^4\)
- \(c\) : distance de la fibre extrême au neutre (si la section est rectangulaire, \(c = \frac{h}{2}\)).
(La valeur de \(c\) n’étant pas donnée, on peut laisser l’expression en fonction de \(c\) ou adopter une valeur hypothétique, par exemple \(c = 0.1\,\text{m}\).)
Calcul
1. Calcul des moments individuels:
- Pour la charge uniformément répartie :
\[ M_{\text{udl}} = \frac{5\,\text{kN/m} \times (6\,\text{m})^2}{8} \] \[ M_{\text{udl}} = \frac{5 \times 36}{8} \] \[ M_{\text{udl}} = \frac{180}{8} \] \[ M_{\text{udl}} = 22.5\,\text{kN}\cdot\text{m} \]
- Pour la charge ponctuelle :
\[ M_{\text{point}} = \frac{10\,\text{kN} \times 6\,\text{m}}{4} \] \[ M_{\text{point}} = \frac{60}{4} = 15\,\text{kN}\cdot\text{m} \]
2. Moment fléchissant total :
\[ M_{\max} = 22.5\,\text{kN}\cdot\text{m} + 15\,\text{kN}\cdot\text{m} \] \[ M_{\max} = 37.5\,\text{kN}\cdot\text{m} \]
(On peut convertir en N\(\cdot\)m : \(37.5\,\text{kN}\cdot\text{m} = 37\,500\,\text{N}\cdot\text{m}\))
3. Contrainte maximale :
\[ \sigma_{\max} = \frac{M_{\max}\,c}{I} = \frac{37\,500\,\text{N}\cdot\text{m}\times c}{4\times10^{-6}\,\text{m}^4} \]
- En fonction de \(c\) :
\[ \sigma_{\max} = 9.375 \times 10^9\, c \quad (\text{en Pa, avec } c \text{ en m}) \]
- Par exemple, si l’on admet \(c = 0.1\,\text{m}\) :
\[ \sigma_{\max} = 9.375 \times 10^9 \times 0.1 \] \[ \sigma_{\max} = 937.5 \times 10^6\,\text{Pa} \] \[ \sigma_{\max} = 937.5\,\text{MPa} \]
Conclusion :
La contrainte maximale de flexion se produit en mi-portée, aux fibres extrêmes (supérieure et inférieure), et s’exprime par :
\[ \sigma_{\max} = \frac{37\,500\,c}{4\times10^{-6}} \quad \text{(Pa)} \]
ou, avec \(c = 0.1\,\text{m}\), environ \(937.5\,\text{MPa}\).
3. Calcul de la déformation maximale de la poutre
La déformation (flèche) maximale d’une poutre simplement appuyée, soumise à plusieurs types de chargement, est obtenue en sommant les contributions de chaque chargement.
Pour :
- Une charge uniformément répartie sur toute la longueur, la flèche maximale est donnée par :
\[ \delta_{\text{udl}} = \frac{5qL^4}{384EI} \]
- Une charge ponctuelle appliquée en milieu de poutre, la flèche maximale est donnée par :
\[ \delta_{\text{point}} = \frac{P L^3}{48EI} \]
La flèche totale est :
\[ \delta_{\max} = \delta_{\text{udl}} + \delta_{\text{point}} \]
Données
- \(L = 6\,\text{m}\)
- \(q = 5\,\text{kN/m} = 5\,000\,\text{N/m}\)
- \(P = 10\,\text{kN} = 10\,000\,\text{N}\)
- \(E = 200\,\text{GPa} = 200 \times 10^9\,\text{N/m}^2\)
- \(I = 4 \times 10^{-6}\,\text{m}^4\)
Calcul
1. Flèche due à la charge uniformément répartie :
- Calcul de \(L^4\) :
\[ L^4 = 6^4 = 1296\,\text{m}^4 \]
- Numérateur :
\[ 5 \times q \times L^4 = 5 \times 5\,000\,\text{N/m} \times 1296 \] \[ = 25\,000 \times 1296 = 32\,400\,000\,\text{N}\cdot\text{m}^3 \]
- Dénominateur :
\[ 384 \times E \times I = 384 \times (200 \times 10^9\,\text{N/m}^2) \times (4 \times 10^{-6}\,\text{m}^4) \]
D’abord, \(200 \times 10^9 \times 4 \times 10^{-6} = 800\,000\,\text{N}\cdot\text{m}^2\).
Ensuite, \(384 \times 800\,000 = 307\,200\,000\).
Ainsi,
\[ \delta_{\text{udl}} = \frac{32\,400\,000}{307\,200\,000} \approx 0.1055\,\text{m} \]
2. Flèche due à la charge ponctuelle :
- Calcul de \(L^3\) :
\[ L^3 = 6^3 = 216\,\text{m}^3 \]
- Numérateur :
\[ P \times L^3 = 10\,000\,\text{N} \times 216 \] \[ = 2\,160\,000\,\text{N}\cdot\text{m}^3 \]
- Dénominateur :
\[ 48 \times E \times I = 48 \times (200 \times 10^9) \times (4 \times 10^{-6}) \]
D’abord, \(200 \times 10^9 \times 4 \times 10^{-6} = 800\,000\).
Ensuite, \(48 \times 800\,000 = 38\,400\,000\).
Ainsi,
\[ \delta_{\text{point}} = \frac{2\,160\,000}{38\,400\,000} \approx 0.0563\,\text{m} \]
3. Flèche maximale totale :
\[ \delta_{\max} = 0.1055\,\text{m} + 0.0563\,\text{m} \] \[ \delta_{\max} \approx 0.1618\,\text{m} \]
Conclusion :
La déformation maximale de la poutre est d’environ :
\[ \delta_{\max} \approx 0.162\,\text{m} \quad \text{(soit environ 16.2 cm)} \]
Charges, contraintes et déformations
D’autres exercices de Rdm :















0 commentaires