Contraintes de Sol par le Cercle de Mohr
Comprendre les Contraintes de Sol par le Cercle de Mohr
Vous êtes un ingénieur géotechnique chargé d’analyser les contraintes dans un échantillon de sol prélevé sur un site de construction prévu pour un immeuble de bureaux. L’échantillon de sol est soumis à un test triaxial pour déterminer ses propriétés mécaniques, notamment sa résistance au cisaillement. Les résultats du test vous fournissent les contraintes principales appliquées sur l’échantillon. Votre tâche est de déterminer les contraintes normales et de cisaillement maximales agissant sur l’échantillon de sol à l’aide du cercle de Mohr.
Pour comprendre le calcul de la Résistance au Cisaillement d’un Sol, cliquez sur le lien.
Données:
- Contrainte principale majeure (\(\sigma_1\)): 150 kPa
- Contrainte principale mineure (\(\sigma_3\)): 50 kPa
- Orientation de l’échantillon: La contrainte principale majeure est verticale.
Questions:
1. Dessiner le cercle de Mohr pour l’échantillon de sol.
2. Calculer la contrainte normale maximale (\(\sigma_{\text{max}}\)).
3. Calculer la contrainte de cisaillement maximale (\(\tau_{\text{max}}\)).
4. Déterminer l’orientation des plans sur lesquels ces contraintes maximales agissent.
Correction : Contraintes de Sol par le Cercle de Mohr
1. Dessin du cercle de Mohr pour l’échantillon du sol
1.1. Calcul du centre et du rayon du Cercle de Mohr
Données :
- Contrainte principale majeure, \(\sigma_1 = 150\) kPa
- Contrainte principale mineure, \(\sigma_3 = 50\) kPa
Formules :
- Centre du cercle, C :
\[ C = \frac{\sigma_1 + \sigma_3}{2} \]
- Rayon du cercle, R :
\[ R = \frac{\sigma_1 – \sigma_3}{2} \]
Calcul :
\[ C = \frac{150 + 50}{2} \] \[ C = \frac{200}{2} \] \[ C = \mathbf{100 \text{ kPa}} \]
\[ R = \frac{150 – 50}{2} \] \[ R = \frac{100}{2} \] \[ R = \mathbf{50 \text{ kPa}} \]
1.2. Dessin du Cercle de Mohr
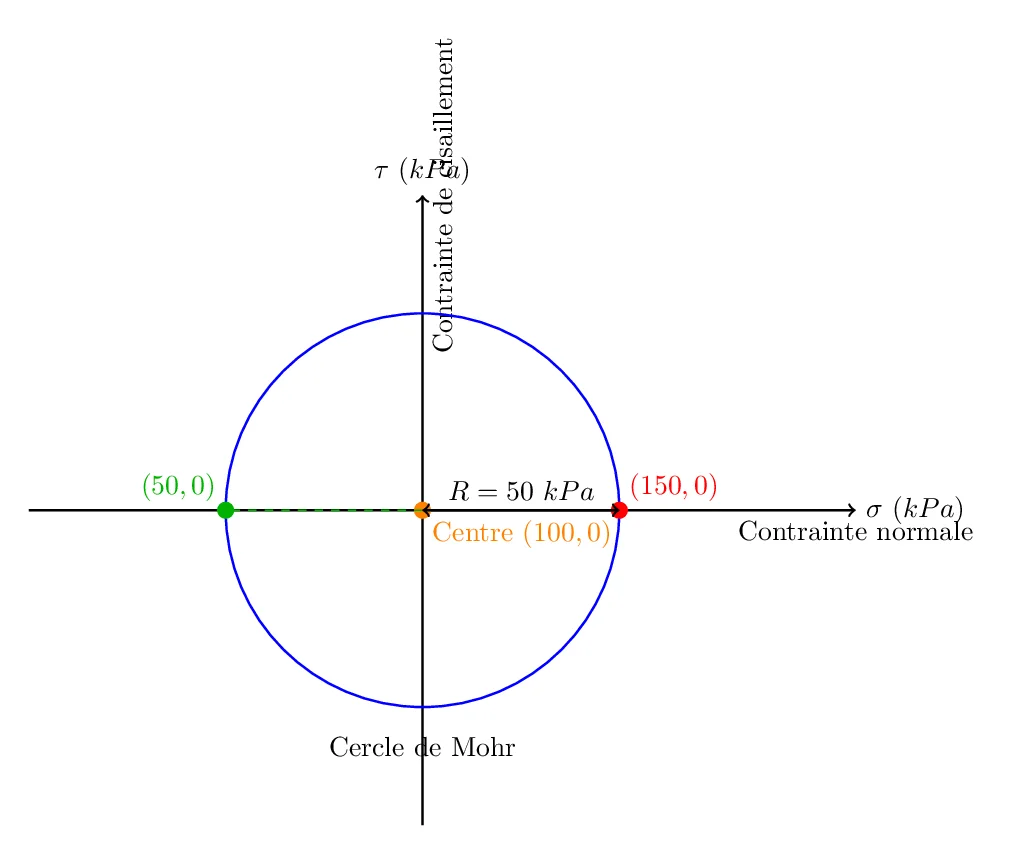
Sur un graphique, l’axe horizontal représente la contrainte normale (σ) et l’axe vertical représente la contrainte de cisaillement (τ).
- Placez le centre du cercle en (100, 0).
- Le cercle passe par les points extrêmes correspondant aux contraintes principales :
- À droite, (σ₁, 0) = (150, 0)
- À gauche, (σ₃, 0) = (50, 0)
- Le rayon du cercle, 50 kPa, définit l’amplitude maximale de la contrainte de cisaillement.
(Schéma : Dessinez un cercle centré en (100, 0) avec un rayon de 50 kPa, incluant les points (150,0) et (50,0).)
2. Calcul des contraintes maximales
a) Contrainte normale maximale (\(\sigma_{\text{max}}\))
La contrainte normale maximale correspond au point le plus à droite sur le cercle de Mohr.
Calcul :
\[ \sigma_{\text{max}} = \text{Centre} + \text{Rayon} \] \[ \sigma_{\text{max}} = 100 + 50 \] \[ \sigma_{\text{max}} = \mathbf{150 \text{ kPa}} \]
b) Contrainte de cisaillement maximale (\(\tau_{\text{max}}\))
La contrainte de cisaillement maximale est égale au rayon du cercle.
Calcul :
\[ \tau_{\text{max}} = \mathbf{50 \text{ kPa}} \]
3. Détermination de l’orientation des plans
Les plans sur lesquels les contraintes maximales agissent se situent selon des orientations spécifiques par rapport aux directions principales :
- Pour la contrainte normale maximale (\(\sigma_{\text{max}}\)) :
Elle se situe sur le plan où la contrainte normale atteint 150 kPa, c’est-à-dire le plan soumis à la contrainte principale majeure (ici verticale puisque \(\sigma_1\) est vertical). - Pour la contrainte de cisaillement maximale (\(\tau_{\text{max}}\)) :
Dans l’analyse par le Cercle de Mohr, les plans sur lesquels agit \(\tau_{\text{max}}\) sont orientés à un angle de 45° par rapport aux directions principales.
Ainsi, si la contrainte principale majeure est verticale, le plan où la contrainte de cisaillement maximale se développe est incliné de 45° par rapport à la verticale (et donc également par rapport à l’horizontale).
Contraintes de Sol par le Cercle de Mohr
D’autres exercices de géotechnique:














0 commentaires