Calculer la variation de longueur des poutres

Comprendre comment Calculer la variation de longueur des poutres

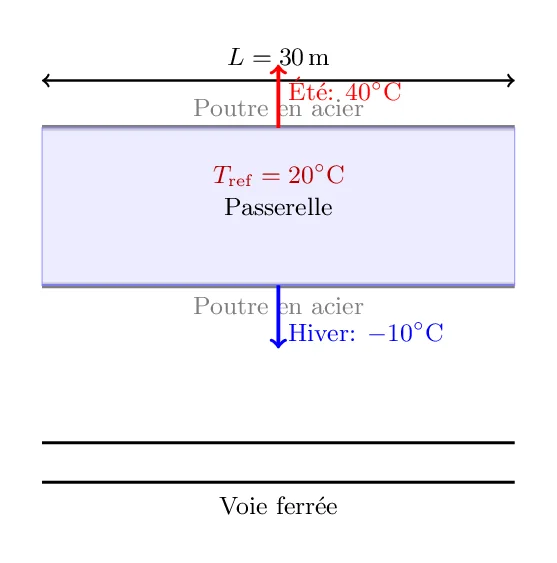
Considérons une passerelle métallique utilisée pour le passage piétonnier au-dessus d’une voie ferrée. La passerelle est soutenue par deux poutres en acier parallèles de longueur L. On souhaite étudier l’influence des variations de température sur cette structure, en particulier lors de conditions extrêmes en été et en hiver.

Pour comprendre la Déformation Axiale Due à la Température, cliquez sur lien.

Données:

Longueur de chaque poutre, L = 30 m
Coefficient de dilatation linéaire de l’acier, \(\alpha = 12 \times 10^{-6}\, /\text{°C}\)
Température en été, \(T_{\text{été}}\) = 40 °C
Température en hiver, \(T_{\text{hiver}}\) = -10 °C
Température de référence lors de l’installation, \(T_{\text{ref}}\) = 20 °C

Question:

Calculer la variation de longueur des poutres en été et en hiver.

Correction : Calculer la variation de longueur des poutres

1. Formule de Base

La variation de longueur d’un matériau soumise à une variation de température est donnée par :

\[ \Delta L = L \times \alpha \times \Delta T \]

avec :

\(L\) : longueur initiale de la poutre,
\(\alpha\) : coefficient de dilatation linéaire,
\(\Delta T = T – T_{\text{ref}}\) : variation de température (température actuelle moins la température de référence).

2. Données de l’Exercice

Longueur de la poutre : \(L = 30\) m,
Coefficient de dilatation linéaire : \(\alpha = 12 \times 10^{-6}\, /^\circ\text{C}\),
Température de référence : \(T_{\text{ref}} = 20^\circ\text{C}\),
Température en été : \(T_{\text{été}} = 40^\circ\text{C}\),
Température en hiver : \(T_{\text{hiver}} = -10^\circ\text{C}\).

3. Calcul de la Variation de Longueur en Été

1. Calcul de la variation de température :

\[ \Delta T_{\text{été}} = T_{\text{été}} – T_{\text{ref}} \] \[ \Delta T_{\text{été}} = 40^\circ\text{C} – 20^\circ\text{C} \] \[ \Delta T_{\text{été}} = 20^\circ\text{C} \]

2. Application de la formule :

\[ \Delta L_{\text{été}} = L \times \alpha \times \Delta T_{\text{été}} \]

En substituant les valeurs :

\[ \Delta L_{\text{été}} = 30\, \text{m} \times 12 \times 10^{-6}\, /^\circ\text{C} \times 20^\circ\text{C} \] \[ \Delta L_{\text{été}} = 30 \times 2.4 \times 10^{-4} \] \[ \Delta L_{\text{été}} = 7.2 \times 10^{-3}\, \text{m} \] \[ \Delta L_{\text{été}} = 0.0072\, \text{m} \quad \text{(soit 7.2 mm d’extension)} \]

4. Calcul de la Variation de Longueur en Hiver

1. Calcul de la variation de température :

\[ \Delta T_{\text{hiver}} = T_{\text{hiver}} – T_{\text{ref}} \] \[ \Delta T_{\text{hiver}} = -10^\circ\text{C} – 20^\circ\text{C} \] \[ \Delta T_{\text{hiver}} = -30^\circ\text{C} \]

2. Application de la formule :

\[ \Delta L_{\text{hiver}} = L \times \alpha \times \Delta T_{\text{hiver}} \]

En substituant les valeurs :

\[ \Delta L_{\text{hiver}} = 30\, \text{m} \times 12 \times 10^{-6}\, /^\circ\text{C} \times (-30^\circ\text{C}) \] \[ \Delta L_{\text{hiver}} = 30 \times (-3.6 \times 10^{-4}) \] \[ \Delta L_{\text{hiver}} = -10.8 \times 10^{-3}\, \text{m} \] \[ \Delta L_{\text{hiver}} = -0.0108\, \text{m} \quad \text{(soit une contraction de 10.8 mm)} \]

Conclusion

En été : la poutre s’allonge de 7.2 mm.
En hiver : la poutre se contracte de 10.8 mm.

Calculer la variation de longueur des poutres

D’autres exercices de Rdm:

Calculer la variation de longueur des poutres