Report des Données Terrain sur Plans
Comprendre le report des Données Terrain sur Plans
Vous êtes un topographe travaillant sur le projet de construction d’une nouvelle route. Avant le début des travaux, il est essentiel de reporter précisément les données du terrain sur le plan de construction.
Vous avez réalisé un levé topographique du site et obtenu les données suivantes, que vous devez maintenant intégrer dans un plan à l’échelle.
Pour comprendre le Calcul de distance en topographie, cliquez sur le lien.
Données Terrain
- Point A : Coordonnées (0, 0), Altitude 50 m
- Point B : Coordonnées (100 m Est, 50 m Nord), Altitude 55 m
- Point C : Coordonnées (50 m Est, 150 m Nord), Altitude 52 m
- Point D : Coordonnées (200 m Est, 100 m Nord), Altitude 58 m
Tâches
- Report des Points sur le Plan : Dessinez un plan à l’échelle 1:1000 en reportant les points A, B, C, et D. Indiquez clairement les coordonnées et altitudes.
- Calcul de Pente : Calculez la pente moyenne entre les points A et B, ainsi qu’entre les points C et D.
- Profil Topographique : Réalisez un profil topographique sur la ligne droite reliant les points A à D. Ce profil doit inclure les points B et C, et montrer les variations d’altitude.
- Surface Planaire : Calculez la surface planaire de la zone délimitée par les points A, B, C, et D.
- Réflexion : Discutez des implications potentielles des variations d’altitude pour le projet de construction de la route. Comment ces informations peuvent-elles influencer les décisions de construction?
Correction : report des Données Terrain sur Plans
1. Report des Points sur le Plan
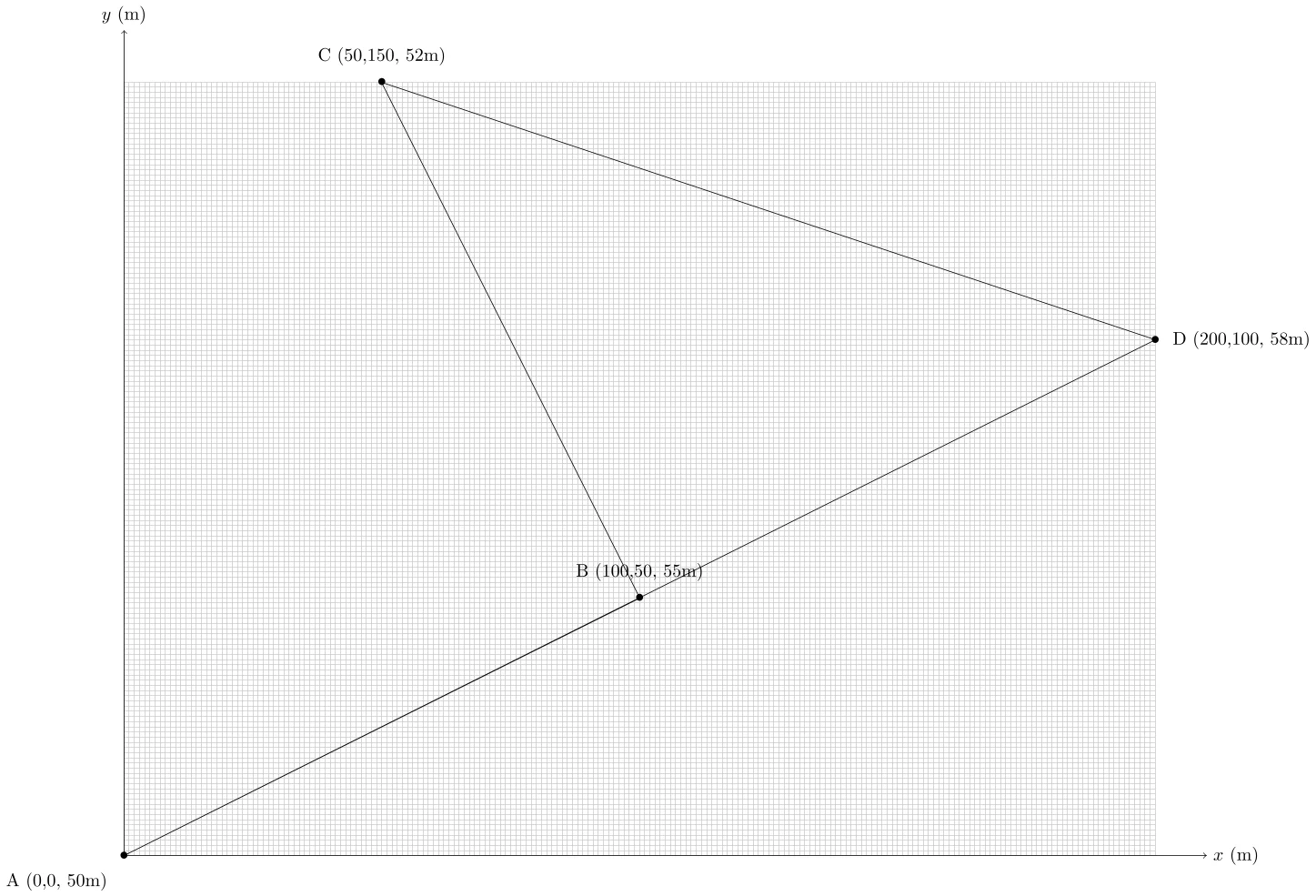
2. Calcul de Pente
Calcul de la pente entre A et B
Calcul de la distance horizontale entre A et B:
\[ d_{AB} = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} \] \[ = \sqrt{(100 – 0)^2 + (50 – 0)^2} \] \[ = \sqrt{10000 + 2500} \] \[ = \sqrt{12500} \] \[ = 111.80 \text{ mètres}
\]
Calcul de la différence d’altitude entre A et B:
\begin{align*}
\Delta h_{AB} &= h_B – h_A \\
&= 55m – 50m \\
&= 5m
\end{align*}
Calcul de la pente:
\[ Pente_{AB} (\%) = \left( \frac{\Delta h_{AB}}{d_{AB}} \right) \times 100 \] \[ = \left( \frac{5}{111.80} \right) \times 100 \] \[ \approx 4.47\% \]
Calcul de la pente entre C et D
Calcul de la distance horizontale entre C et D:
\[ d_{CD} = \sqrt{(x_D – x_C)^2 + (y_D – y_C)^2} \] \[ = \sqrt{(200 – 50)^2 + (100 – 150)^2} \] \[ = \sqrt{15000 + 2500} \] \[ = \sqrt{17500} \] \[ = 132.29 \text{ mètres}
\]
Calcul de la différence d’altitude entre C et D:
\begin{align*}
\Delta h_{CD} &= h_D – h_C \\
&= 58m – 52m \\
&= 6m
\end{align*}
Calcul de la pente:
\[ Pente_{CD} (\%) = \left( \frac{\Delta h_{CD}}{d_{CD}} \right) \times 100 \] \[ = \left( \frac{6}{132.29} \right) \times 100 \] \[ \approx 4.54\% \]
Ces calculs montrent que la pente entre les points A et B est d’environ 4.47% et entre C et D d’environ 4.54%.
Ces valeurs indiquent la pente du terrain entre ces points, ce qui est une information essentielle pour la planification de projets de génie civil comme la construction de routes
3. Profil Topographique
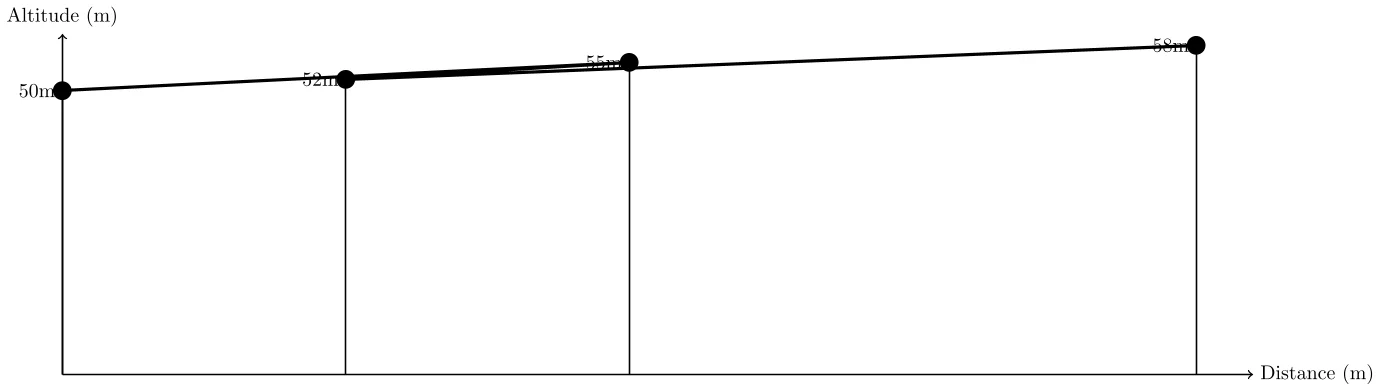
4. Calcul de Surface Planaire
Pour calculer la surface planaire, nous avons utilisé la formule de Héron pour deux triangles hypothétiques formés par les points A, B, C et D.
Distances entre les points :
\[ AB = \sqrt{100^2 + 50^2} \] \[ AB = 111.80 \text{ m} \]
\[ AC = \sqrt{50^2 + 150^2} \] \[ AC = 158.11 \text{ m} \]
\[ AD = \sqrt{200^2 + 100^2} \] \[ AD = 223.61 \text{ m} \]
\[ BC = \sqrt{(100 – 50)^2 + (50 – 150)^2} \] \[ BC = 111.80 \text{ m} \]
\[ BD = \sqrt{(200 – 100)^2 + (100 – 50)^2} \] \[ BD = 158.11 \text{ m} \]
\[ CD = \sqrt{(200 – 50)^2 + (100 – 150)^2} \] \[ CD = 158.11 \text{ m}
\]
Aire des triangles :
- Pour le triangle ABD :
\[ s_{ABD} = \frac{AB + AD + BD}{2} \] \[ s_{ABD} = 246.76 \text{ m} \]
\(\text{Aire}_{ABD} = \sqrt{s_{ABD}(s_{ABD} – AB)(s_{ABD} – AD)(s_{ABD} – BD)}\)
\[ = 6250 \text{ m}^2 \text{ (arrondie)}
\]
- Pour le triangle BCD :
\(\text{Aire}_{BCD} = \text{Aire}_{ABD} = 6250 \text{ m}^2 \text{ (par symétrie)}\)
Aire totale :
\[ \text{Aire}_{\text{totale}} = \text{Aire}_{ABD} + \text{Aire}_{BCD} \]
\[ = 12500 \text{ m}^2
\]
5. Réflexion sur les Variations d’Altitude
En ce qui concerne les implications des variations d’altitude pour le projet de construction de la route :
- Des altitudes plus élevées peuvent nécessiter plus de terrassement, influençant le coût et le calendrier du projet.
- Les zones de haute altitude peuvent être plus exposées à des conditions météorologiques extrêmes, affectant la durabilité de la route.
- Les pentes raides doivent être atténuées pour assurer la sécurité des véhicules, ce qui peut nécessiter des murs de soutènement ou des coupes dans le paysage.
- Des considérations doivent être prises pour le drainage de l’eau de surface afin de prévenir l’érosion.
- Les zones basses peuvent être sujettes à l’accumulation d’eau, nécessitant un drainage adéquat pour éviter la formation de zones humides.
- L’impact visuel du projet doit être pris en compte; les routes doivent s’intégrer harmonieusement dans le paysage naturel.
Report des Données Terrain sur Plans
D’autres exercices de topographie:







0 commentaires