Facteur de Sécurité et Glissements de Terrain
Comprendre le Facteur de Sécurité et Glissements de Terrain
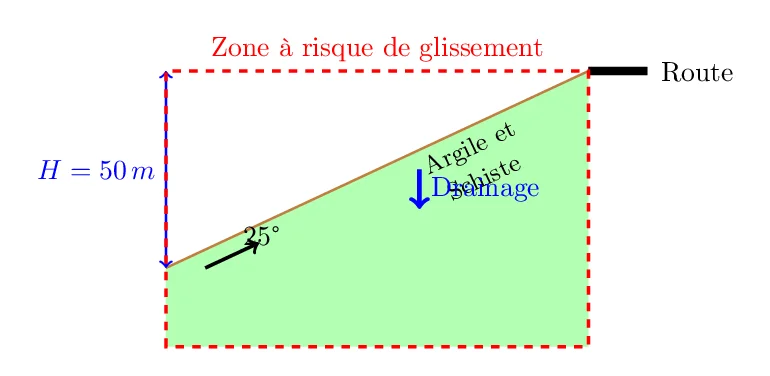
Un projet de construction d’une route traverse une zone à risque de glissement de terrain située dans une région montagneuse. L’objectif est de réaliser une analyse de stabilité pour évaluer le risque de glissement de terrain avant le début des travaux. La pente concernée est composée principalement d’argile et de schiste.
Pour comprendre l’Analyse de la stabilité d’une pente, cliquez sur le lien.
Données fournies:
- Angle de la pente: 25°
- Cohésion du sol (C): 15 kPa
- Angle de frottement interne (φ): 20°
- Hauteur de la pente (H): 50 m
- Densité du sol (ρ): 1800 kg/m³
- Teneur en eau du sol: 22%
- Facteur de sécurité désiré: 1.5
Considérations supplémentaires:
- La région a une histoire de précipitations élevées, ce qui pourrait augmenter la teneur en eau du sol et réduire la cohésion.
- Un drainage est envisagé pour réduire la pression de l’eau interstitielle.
Questions:
Calculer le facteur de sécurité contre le glissement de terrain en utilisant la méthode de Bishop simplifiée. Estimer l’effet d’une augmentation de 10% de la teneur en eau sur le facteur de sécurité.
Correction: Facteur de Sécurité et Glissements de Terrain
Pour cette correction, nous ferons les hypothèses et approximations suivantes :
- On considère un glissement par une surface circulaire dont la longueur est assimilée à la longueur de la pente.
- L’analyse se fait pour une largeur unitaire (1 m) en section verticale.
- La méthode simplifiée consiste à écrire le bilan des forces résistantes (résistance due à la cohésion et au frottement) par rapport à la force motrice (composante gravitationnelle parallèle à la pente).
- On négligera, pour simplifier, l’effet de la distribution variable des pressions interstitielles et on supposera initialement un sol « sec » (u = 0) pour le calcul de base.
- L’augmentation de la teneur en eau sera modélisée par une réduction proportionnelle (ici 10 %) de la cohésion et de la résistance au frottement (puisque la pression interstitielle augmente, la contrainte normale effective diminue).
Remarque sur la méthode : La méthode de Bishop simplifiée est habituellement itérative avec découpage en tranches. Ici, pour obtenir une première estimation, nous utiliserons une formulation globale « équivalente ».
1. Calcul de la résistance totale
La résistance totale \( R \) se compose de deux contributions :
- La résistance cohésive \( R_c \)
- La résistance par frottement \( R_f \)
1.1. Résistance cohésive
On suppose que la cohésion s’exerce sur toute la longueur \( L \) de la surface de glissement.
Formule :
\[ R_c = c \times L \]
Données :
Cohésion, \( c = 15\ \text{kPa} = 15\,000\ \text{N/m}^2 \)
Longueur de la pente (que nous assimilons à la surface de glissement)
\[ L = \frac{H}{\sin(\theta)} \]
- Hauteur, \( H = 50\ \text{m} \)
- Angle de la pente, \( \theta = 25^\circ \)
Avec \[ \sin(25^\circ) \approx 0.4226 \]
Calcul :
\[ L = \frac{50}{0.4226} \approx 118.3\ \text{m} \]
\[ R_c = 15\,000\ \text{N/m}^2 \times 118.3\ \text{m} \] \[ R_c \approx 1\,774\,500\ \text{N} \]
1.2. Résistance par frottement
La résistance au frottement dépend de la composante normale effective et de l’angle de frottement interne.
Formule simplifiée :
\[ R_f = N \times \tan(\phi) \]
où, pour une estimation globale, la force normale moyenne \( N \) est liée à la composante du poids perpendiculaire à la pente. Pour un sol de densité \( \rho \) et en considérant la totalité du poids du sol susceptible de glisser, on utilise une estimation du poids total \( W \) et on prend \( N \approx W \cos(\theta) \).
Calcul du poids total \( W \) :
- Volume approximé de la masse de sol en glissement :
Pour une largeur unitaire, on approxime l’aire du profil de la pente par le triangle dont l’aire est :
\[ A = \frac{1}{2} \times H \times L \] \[ A = \frac{1}{2} \times 50\ \text{m} \times 118.3\ \text{m} \] \[ A \approx 2960\ \text{m}^2 \]
- Poids par unité de largeur :
La masse volumique (poids volumique) se calcule par :
\[ \gamma = \rho \times g \] avec \(\rho = 1800\ \text{kg/m}^3 \text{ et } g=9.81\ \text{m/s}^2\)
\[ \gamma = 1800 \times 9.81 \] \[ \gamma \approx 17\,658\ \text{N/m}^3 \]
Ainsi,
\[ W = \gamma \times A \] \[ W \approx 17\,658\ \text{N/m}^3 \times 2960\ \text{m}^2 \] \[ W \approx 52\,220\,000\ \text{N} \]
Données supplémentaires pour le frottement :
- Angle de frottement, \( \phi = 20^\circ \)
avec \( \tan(20^\circ) \approx 0.3640 \)
- \( \cos(25^\circ) \approx 0.9063 \)
Calcul :
\[ N \approx W \cos(\theta) \] \[ N \approx 52\,220\,000 \times 0.9063 \] \[ N \approx 47\,361\,000\ \text{N} \]
\[ R_f = 47\,361\,000\ \text{N} \times 0.3640 \] \[ R_f \approx 17\,244\,000\ \text{N} \]
1.3. Résistance totale (\( R \))
\[ R = R_c + R_f \] \[ R \approx 1\,774\,500 + 17\,244\,000 \] \[ R \approx 19\,018\,500\ \text{N} \]
2. Calcul de la force motrice (\( D \))
La force motrice est la composante du poids qui tend à faire glisser le sol.
Formule :
\[ D = W \times \sin(\theta) \]
Données :
- \( \sin(25^\circ) \approx 0.4226 \)
Calcul :
\[ D = 52\,220\,000\ \text{N} \times 0.4226 \] \[ D \approx 22\,066\,000\ \text{N} \]
3. Calcul du facteur de sécurité (\( FS \))
Le facteur de sécurité se définit comme le rapport entre la résistance totale et la force motrice.
Formule :
\[ FS = \frac{R}{D} \]
Calcul :
\[ FS = \frac{19\,018\,500}{22\,066\,000} \] \[ FS \approx 0.861 \]
Interprétation :
Ce résultat indique que le facteur de sécurité est inférieur à la valeur désirée de 1,5, ce qui suggère que, dans l’état initial (avec les données fournies et sans dispositif de renforcement), la pente présente un risque élevé de glissement.
4. Effet d’une augmentation de 10% de la teneur en eau
L’augmentation de la teneur en eau a pour effet de :
- Réduire la cohésion effective : La cohésion diminue à cause de l’augmentation des pressions interstitielles.
- Réduire la résistance au frottement : La réduction de la contrainte normale effective diminue l’effet du frottement.
Hypothèse simplifiée :
Une augmentation de 10 % de la teneur en eau est supposée entraîner une réduction de 10 % de la cohésion et de la résistance par frottement.
4.1. Nouvelle résistance cohésive
- Nouvelle cohésion :
\[ c_{\text{nouveau}} = 15\,000\ \text{N/m}^2 \times 0.90 \] \[ c_{\text{nouveau}} = 13\,500\ \text{N/m}^2 \]
- Calcul de \( R_{c,\text{nouveau}} \) :
\[ R_{c,\text{nouveau}} = 13\,500\ \text{N/m}^2 \times 118.3\ \text{m} \] \[ R_{c,\text{nouveau}} \approx 1\,600\,050\ \text{N} \]
4.2. Nouvelle résistance par frottement
On suppose que la résistance par frottement diminue également de 10% :
\[ R_{f,\text{nouveau}} = 17\,244\,000\ \text{N} \times 0.90 \] \[ R_{f,\text{nouveau}} \approx 15\,519\,600\ \text{N} \]
4.3. Nouvelle résistance totale
\[ R_{\text{nouveau}} = R_{c,\text{nouveau}} + R_{f,\text{nouveau}} \] \[ R_{\text{nouveau}} \approx 1\,600\,050 + 15\,519\,600 \] \[ R_{\text{nouveau}} \approx 17\,119\,650\ \text{N} \]
4.4. Nouveau facteur de sécurité
La force motrice \( D \) reste (pour cette estimation) inchangée : \( 22\,066\,000\ \text{N} \).
\[ FS_{\text{nouveau}} = \frac{17\,119\,650}{22\,066\,000} \] \[ FS_{\text{nouveau}} \approx 0.775 \]
Interprétation :
L’augmentation de 10 % de la teneur en eau réduit le facteur de sécurité de 0,861 à environ 0,775, accentuant ainsi le risque de glissement.
Conclusion
- État initial :
Le facteur de sécurité calculé est d’environ 0,861, bien en dessous de la valeur désirée de 1,5. - Après augmentation de 10 % de la teneur en eau :
Le FS chute à environ 0,775, ce qui démontre l’effet délétère de l’humidité accrue sur la stabilité de la pente.
Ces résultats montrent que, dans les conditions initiales et encore plus après une augmentation de la teneur en eau, la pente présente un risque significatif de glissement. Des mesures de stabilisation (comme le drainage envisagé ou d’autres renforcements) seront indispensables pour atteindre ou dépasser le facteur de sécurité requis.
Note : Les calculs présentés ici reposent sur des approximations et des simplifications (notamment l’hypothèse d’une surface de glissement coïncidant avec la pente et l’application directe d’une formule globale) propres à une approche pédagogique. Dans une étude professionnelle, la méthode de Bishop simplifiée impliquerait un découpage en tranches et une résolution itérative afin d’obtenir une évaluation plus précise du FS.
Facteur de Sécurité et Glissements de Terrain
D’autres exercices de Géotechnique:














0 commentaires