Cisaillement simple d’un axe

Comprendre le Cisaillement simple d’un axe

Un bureau d’études en génie civil travaille sur la conception d’un nouveau bâtiment. L’une des étapes clés du projet consiste à évaluer la résistance d’un axe en acier utilisé dans la structure de support d’une passerelle piétonne. Cet axe est soumis à des forces transversales dues au poids des piétons et à l’équipement installé sur la passerelle. Pour garantir la sécurité et la durabilité de la structure, il est crucial de vérifier que cet axe peut résister aux efforts de cisaillement induits sans subir de déformation plastique.

Pour comprendre la Déformation Axiale Due à la Température, cliquez sur le lien.

Données:

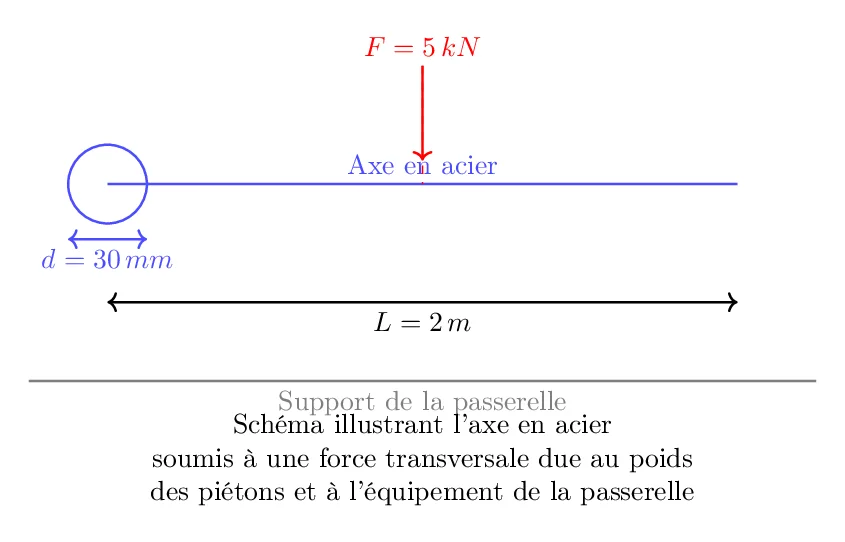
Diamètre de l’axe en acier (d): 30 mm
Longueur de l’axe (L): 2 m
Force transversale appliquée (F): 5 kN (direction perpendiculaire à l’axe de l’élément)
Module de Coulomb de l’acier (G): 81 GPa (information supplémentaire pour des calculs de déformation, si nécessaire)
Coefficient de sécurité (n): 3

Questions:

1. Calcul de la surface de cisaillement (A):

Déterminer la surface de l’axe en acier soumise au cisaillement.

2. Calcul de la contrainte de cisaillement (τ) dans l’axe

3. Analyse de la sécurité:

Comparer la contrainte de cisaillement obtenue avec la contrainte admissible pour l’acier utilisé, en considérant le coefficient de sécurité.
Note: La contrainte de cisaillement maximale pour l’acier est typiquement autour de 260 à 300 MPa

4. Conclusion: Sur la base des résultats obtenus, conclure si l’axe en acier est apte à résister aux efforts de cisaillement sans défaillance.

Correction : Cisaillement simple d’un axe

1. Calcul de la Surface de Cisaillement (A)

On considère ici que la force de cisaillement est distribuée uniformément sur la section circulaire de l’axe. La surface de la section (A) est obtenue par la formule de l’aire d’un cercle.

Formule :

\[ A = \frac{\pi}{4} \times d^2 \]

Données :

Diamètre d = 30 mm = 0,03 m

Calcul :

\[ A = \frac{\pi}{4} \times (0,03)^2 \] \[ A = \frac{\pi}{4} \times 0,0009 \] \[ A \approx 0,0007069\ \text{m}^2 \]

2. Calcul de la Contrainte de Cisaillement (\(\tau\))

La contrainte de cisaillement est déterminée en divisant la force appliquée par la surface sur laquelle cette force agit.

Formule :

\[ \tau = \frac{F}{A} \]

Données :

Force transversale \(F = 5\ \text{kN} = 5000\ \text{N}\)
Surface \(A \approx 0,0007069\ \text{m}^2\) (calculée précédemment)

Calcul :

\[ \tau = \frac{5000\ \text{N}}{0,0007069\ \text{m}^2} \] \[ \tau \approx 7\,074\ \text{N/m}^2 \quad \text{soit} \quad \tau \approx 7,07\ \text{MPa} \]

3. Analyse de la Sécurité

Pour vérifier la sécurité, il faut comparer la contrainte de cisaillement calculée (\(\tau\)) avec la contrainte admissible de l’acier, en tenant compte du coefficient de sécurité.

Données :

Contrainte maximale pour l’acier : environ 260 à 300 MPa
Coefficient de sécurité n = 3

Calcul de la contrainte admissible réduite :

On considère la contrainte admissible effective :

\[ \tau_{\text{admissible}} = \frac{\tau_{\text{max}}}{n} \]

En prenant la limite inférieure (260 MPa) pour être conservateur :

\[ \tau_{\text{admissible}} = \frac{260\ \text{MPa}}{3} \approx 86,67\ \text{MPa} \]

Comparaison :

Contrainte calculée : \(\approx 7,07\ \text{MPa}\)
Contrainte admissible (avec coefficient de sécurité) : \(\approx 86,67\ \text{MPa}\)

Le rapport de sécurité est donc très confortable puisque 7,07 MPa est bien inférieur à 86,67 MPa.

4. Conclusion

Sur la base des résultats obtenus :

Surface de cisaillement (A) : ≈ 0,0007069 m²
Contrainte de cisaillement (τ) : ≈ 7,07 MPa
Contrainte admissible corrigée : ≈ 86,67 MPa

L’axe en acier, soumis à une force de cisaillement de 5 kN, génère une contrainte de cisaillement bien inférieure à la limite admise (même après application du coefficient de sécurité). Ainsi, l’axe est apte à résister aux efforts de cisaillement sans risque de défaillance.

Cisaillement simple d’un axe

D’autres exercices de Rdm: