Capacité Portante d’une Fondation
Comprendre la Capacité Portante d’une Fondation
Dans une zone rurale, un ingénieur civil est chargé de concevoir les fondations pour une nouvelle école. Le sol est principalement composé d’argile avec une couche de sable à une certaine profondeur. La fondation prévue est une semelle continue sous un mur porteur.
Données:
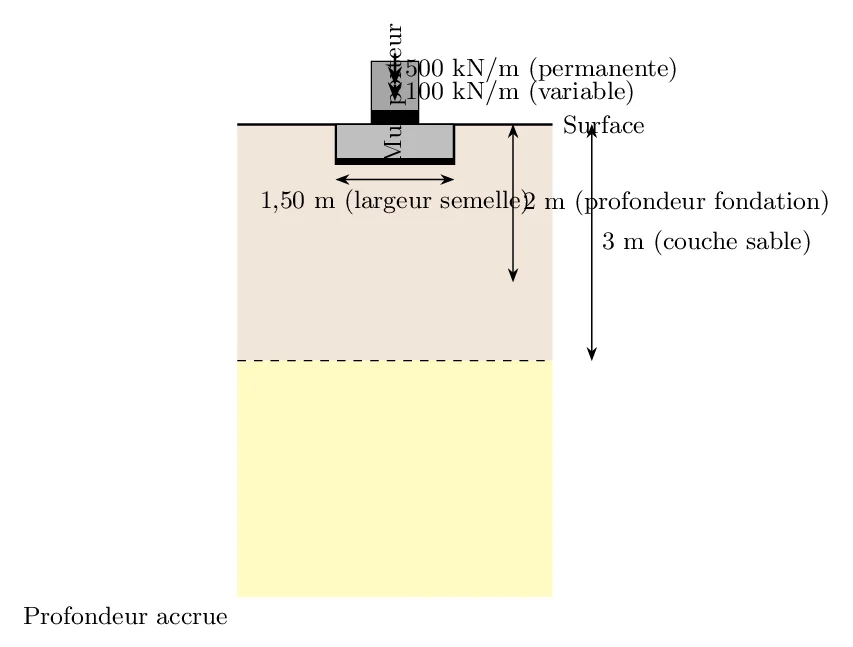
- Profondeur de la fondation : 2 mètres
- Largeur de la fondation : 1,5 mètres
- Poids de la structure (charge permanente) : 500 kN/m
- Poids des équipements (charge variable) : 100 kN/m
- Caractéristiques du sol :
- Argile : Cohésion (c) = 25 kPa, Angle de frottement interne (φ) = 0°
- Sable : Cohésion (c) = 0 kPa, Angle de frottement interne (φ) = 30°
- Profondeur de la couche de sable : 3 mètres sous la surface
Questions:
1. Calculer la capacité portante ultime du sol sous la fondation.
2. Déterminer si la fondation est adéquate pour les charges données en tenant compte des facteurs de sécurité.
3. Suggérer des améliorations ou modifications de la conception si nécessaire.
Correction : Capacité Portante d’une Fondation
1. Calcul de la capacité portante ultime \((q_{ult})\)
La capacité portante ultime (\(q_{ult}\)) est la contrainte maximale que le sol peut supporter avant rupture. Pour une semelle filante en sol cohésif (φ = 0°), on utilise la formule simplifiée de Terzaghi :
Formule
\[ q_{ult} = c\,N_c + q\,N_q + 0.5\,\gamma\,B\,N_\gamma \]
Données
| Paramètre | Valeur | Unité | Source / Note |
|---|---|---|---|
| Cohésion, c | 25 | kPa | donnée |
| Facteur de capacité Nc | 5,14 | – | φ=0° |
| Facteur de capacité Nq | 1 | – | φ=0° |
| Facteur de capacité Nγ | 0 | – | φ=0° |
| Profondeur fondation, Df | 2 | m | donnée |
| Largeur fondation, B | 1,50 | m | donnée |
| Poids volumique de l’argile, γ_argile | 18 | kN/m³ | valeur typique |
| Contrainte due au surpoids q = γ_argile·Df | 36 | kPa | calcul |
Calcul détaillé
- \(c\,N_c = 25 \times 5.14 = 128.50 \text{ kPa}\)
- \(q\,N_q = 36 \times 1 = 36.00 \text{ kPa}\)
- \(0.5\,\gamma\,B\,N_\gamma = 0.5 \times 18 \times 1.5 \times 0 = 0 \text{ kPa}\)
\[ q_{ult} = 128.50 + 36.00 + 0 \] \[ q_{ult} = 164.50 \text{ kPa} \]
2. Calcul de la capacité portante admissible \((q_{all})\)
On divise \(q_{ult}\) par un facteur de sécurité (FS) pour obtenir la capacité admissible.
Formule
\[ q_{all} = \frac{q_{ult}}{FS} \]
Données
| Paramètre | Valeur | Unité |
|---|---|---|
| qult | 164,50 | kPa |
| FS | 3 | – |
Calcul
\[ q_{all} = \frac{164.50}{3} = 54.83 \text{ kPa} \]
3. Calcul de la pression appliquée (\(q_{appl}\))
La pression appliquée est la charge totale par mètre linéaire divisée par l’aire de la semelle (B × 1 m).
Formule
\[ q_{appl} = \frac{P_{perm} + P_{var}}{B} \]
Données
| Paramètre | Valeur | Unité |
|---|---|---|
| Charge permanente | 500 | kN/m |
| Charge variable | 100 | kN/m |
| B | 1,50 | m |
Calcul
\[ q_{appl} = \frac{500 + 100}{1.50} \] \[ q_{appl} = \frac{600}{1.50} \] \[ q_{appl} = 400.00 \text{ kPa} \]
4. Vérification de l’adéquation
\[ q_{appl} = 400.00 \text{ kPa} > q_{all} = 54.83 \text{ kPa} \]
Conclusion : La fondation n’est pas adéquate (pression appliquée >> capacité admissible).
5. Suggestions d’amélioration
| Option | Description | Calcul rapide | Résultat |
|---|---|---|---|
| Fondations profondes | Reposer sur la couche de sable (φ=30°, γ=20 kN/m³) à 3 m | qₙᵤₗₜ(sable) ≈ 1 440 kPa → q_all ≈ 480 kPa | q_appl (400 kPa) < 480 kPa ✅ |
| Agrandissement de la semelle | Réduire q_appl en augmentant B | B_min = 600 / 54,83 ≈ 10,94 m | Peu réaliste |
| Pieux | Transfert de charge vers couches profondes | — | Solution courante |
Recommandation principale : creuser jusqu’à la couche de sable et construire la semelle sur sable, assurant \(q_{all}\) ≈ 480 kPa > 400 kPa.
Capacité Portante d’une Fondation
D’autres exerecices de fondation:










0 commentaires