Calcul des Contraintes Principales
Comprendre le calcul des Contraintes Principales
Dans un projet de construction d’un pont, les ingénieurs doivent évaluer la sécurité de la structure sous différentes charges.
Un élément structurel clé, une poutre en acier, est soumis à des contraintes dues à la charge du trafic et aux conditions environnementales.
Pour comprendre l’Analyse des Contraintes par le Cercle de Mohr, cliquez sur le lien.
Données
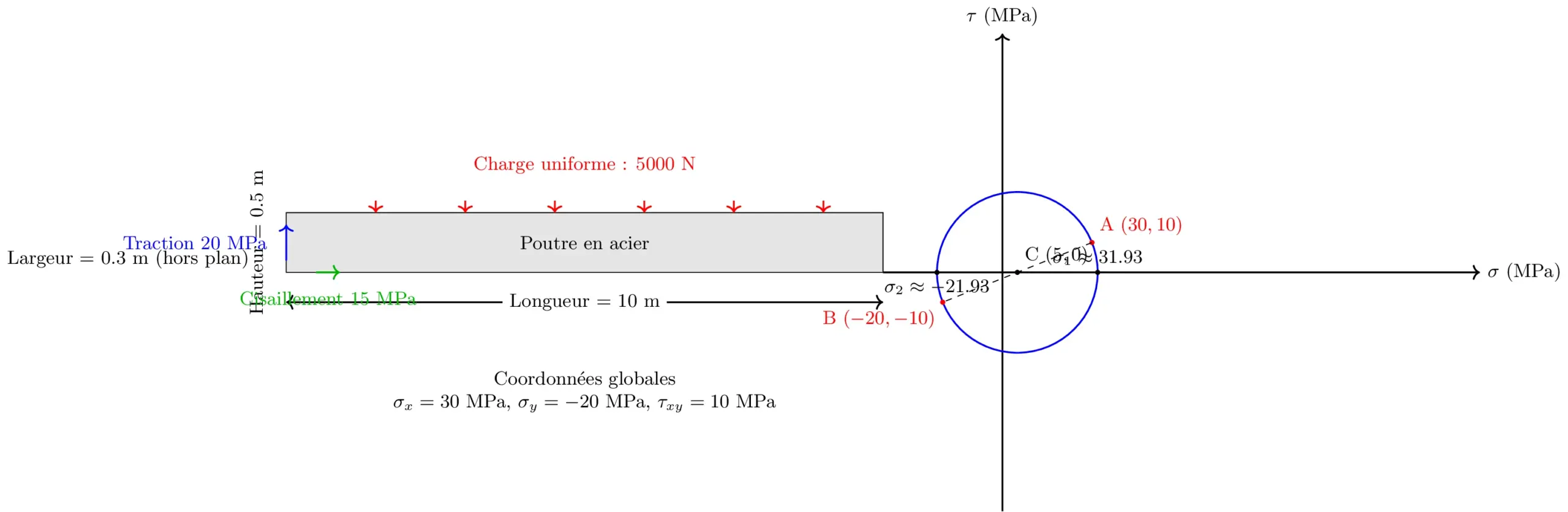
- Dimensions de la poutre : Longueur = 10 m, Largeur = 0.3 m, Hauteur = 0.5 m.
- Matériau : Acier, avec une limite d’élasticité de 250 MPa.
- Charge appliquée : 5000 N répartis uniformément sur toute la longueur de la poutre.
- Contraintes supplémentaires dues aux conditions environnementales : 20 MPa en traction et 15 MPa en cisaillement.
- Coordonnées des contraintes dans le système global : \(
\sigma_x = 30 \, \text{MPa}, \quad \sigma_y = -20 \, \text{MPa}, \quad \tau_{xy} = 10 \, \text{MPa}.
\)
Questions:
Déterminer les contraintes principales (\(\sigma_1\) et \(\sigma_2\)) et les directions principales dans la poutre.
Correction : calcul des Contraintes Principales
Étape 1 : Calcul des Contraintes dues à la Charge Appliquée
La charge appliquée est de 5000 N répartis uniformément sur la longueur de la poutre (10 m). Nous calculons d’abord la contrainte normale due à cette charge.
- L’aire de la section transversale de la poutre est:
\[
A = \text{largeur} \times \text{hauteur} \] \[
A = 0.3 \, m \times 0.5 \, m \] \[
A = 0.15 \, m^2.
\]
- La contrainte normale due à la charge appliquée est:
\[
\sigma = \frac{\text{Force}}{\text{Aire}} = \frac{5000 \, N}{0.15 \, m^2} \] \[
\sigma = 33333.33 \, \text{Pa} = 33.33 \, \text{MPa}.
\]
Étape 2 : Ajout des Contraintes Environnementales
Les contraintes environnementales données sont 20 MPa en traction et 15 MPa en cisaillement. Ainsi, les contraintes totales dans le système global sont :
\[
\sigma_x = 30 \, \text{MPa} + 33.33 \, \text{MPa} \] \[
\sigma_x = 63.33 \, \text{MPa}
\]
\[
\sigma_y = -20 \, \text{MPa}
\]
\[
\tau_{xy} = 10 \, \text{MPa} + 15 \, \text{MPa} \] \[
\tau_{xy} = 25 \, \text{MPa}
\]
Étape 3 : Utilisation des Équations de Transformation des Contraintes
Les équations de transformation ne sont pas nécessaires dans cet exercice car les contraintes sont déjà données dans le système global.
Étape 4 : Calcul des Contraintes Principales
Les contraintes principales \(\sigma_1\) et \(\sigma_2\) sont données par :
\[\sigma_1, \sigma_2 = \frac{\sigma_x + \sigma_y}{2} \pm \sqrt{\left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2}\]
Avec les valeurs données :
\begin{align*}
\sigma_x &= 63.33 \, \text{MPa} \\
\sigma_y &= -20 \, \text{MPa} \\
\tau_{xy} &= 25 \, \text{MPa}
\end{align*}
1. Calcul de la Moyenne des Contraintes (\(\sigma_{\text{avg}}\))
La moyenne des contraintes (\(\sigma_{\text{avg}}\)) est la moyenne arithmétique de \(\sigma_x\) et \(\sigma_y\).
\[
\sigma_{\text{avg}} = \frac{\sigma_x + \sigma_y}{2} \] \[
\sigma_{\text{avg}} = \frac{63.33 – 20}{2} \] \[
\sigma_{\text{avg}} = \frac{43.33}{2} = 21.665 \, \text{MPa}
\]
2. Calcul de \(R\)
\(R\) est la racine carrée de la somme du carré de la moitié de la différence entre \(\sigma_x\) et \(\sigma_y\), et du carré de \(\tau_{xy}\).
\[
R = \sqrt{\left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2} \] \[
R = \sqrt{\left( \frac{63.33 + 20}{2} \right)^2 + 625} \] \[
R = \sqrt{2083.33 + 625} \] \[
R = 48.59 \, \text{MPa}
\]
3. Calcul des Contraintes Principales (\(\sigma_1\) et \(\sigma_2\))
Les contraintes principales sont calculées en ajoutant et soustrayant \(R\) de \(\sigma_{\text{avg}}\).
\[ \sigma_1 = \sigma_{\text{avg}} + R \] \[ \sigma_1 = 21.665 + 48.59 \] \[ \sigma_1 = 70.25 \, \text{MPa} \]
\[ \sigma_2 = \sigma_{\text{avg}} – R \] \[ \sigma_1 = 21.665 – 48.59 \] \[ \sigma_2 = -26.92 \, \text{MPa}
\]
Contrainte principale 1: \[ (\sigma_1) = 70.25 \text{ MPa} \]
Contrainte principale 2: \[ (\sigma_2) = -26.92 \text{ MPa} \]
Étape 5 : Détermination des Angles des Directions Principales
Les angles des directions principales \((\theta_p)\) par rapport à l’axe global sont donnés par la formule suivante :
\[
\tan(2\theta_p) = \frac{2\tau_{xy}}{\sigma_x – \sigma_y}
\]
où \(\sigma_x\) et \(\sigma_y\) sont les contraintes normales dans les directions x et y, respectivement, et \(\tau_{xy}\) est la contrainte de cisaillement.
L’angle de la direction principale par rapport à l’axe global \(\theta_p\) = 15.48°
Vérification de la Sécurité
- La contrainte principale la plus élevée est 70.25 MPa, ce qui est bien en dessous de la limite d’élasticité de l’acier (250 MPa). Cela indique que sous les charges et conditions données, la poutre est en sécurité et ne risque pas de dépasser sa limite d’élasticité.
Conclusion
- Les résultats montrent que la poutre peut supporter les charges et contraintes appliquées sans risque de défaillance structurelle.
- L’angle de 15.48° indique l’orientation des contraintes principales par rapport à l’axe global, une information cruciale pour la conception et l’analyse détaillée de la structure.
- Cette analyse aide les ingénieurs à comprendre le comportement de la structure sous charge et à prendre des décisions éclairées concernant la conception et la sécurité du pont.
Calcul des Contraintes Principales
D’autres exercices de Rdm:
0 commentaires