Calcul de Volume pour un Talus
Comprendre le Calcul de Volume pour un Talus
Vous êtes ingénieur civil travaillant sur un projet de construction d’une nouvelle route dans une région vallonnée. Pour minimiser l’impact environnemental et optimiser l’utilisation du terrain, vous avez décidé d’utiliser un système de talus en terrasse pour stabiliser les pentes adjacentes à la route. Le design du talus doit suivre un ratio de pente de 3 pour 2 (horizontal pour vertical).
Pour comprendre le Calcul d’un Talus en Terrassement, cliquez sur le lien.
Données:
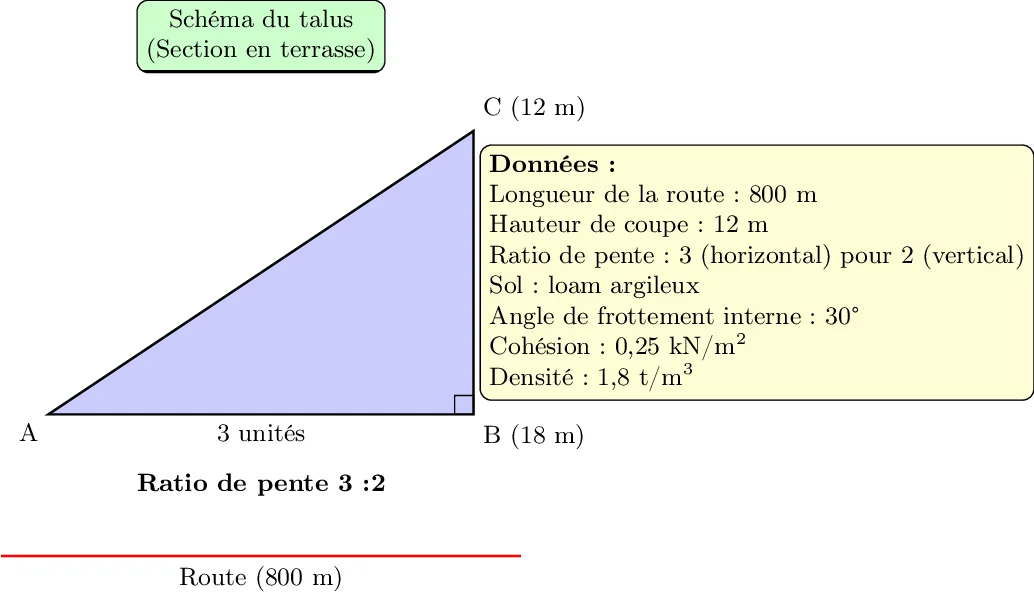
- Longueur totale de la route : 800 mètres.
- Hauteur moyenne de la coupe nécessaire pour l’installation de la route : 12 mètres.
- Le sol est principalement composé de loam argileux, avec un angle de frottement interne de 30 degrés et une cohésion de 0,25 kN/m².
- La densité du sol est de 1,8 t/m³.
- Le talus forme un triangle droit.
Questions:
1. Calcul de la longueur du talus : Déterminez la longueur horizontale nécessaire pour chaque segment du talus en utilisant le ratio de pente de 3 pour 2. Rappelons que le ratio signifie que pour chaque 2 mètres verticaux, le talus s’étend de 3 mètres horizontalement.
2. Volume du terrassement : Calculez le volume total de terre à déplacer pour créer le talus.
3. Stabilité du talus : Évaluez la stabilité du talus en utilisant l’angle de frottement interne et la cohésion du sol. Assurez-vous que l’angle du talus est sécuritaire par rapport à l’angle de frottement interne du sol.
4. Estimation des coûts : Fournissez une estimation des coûts associés au déplacement du volume de terre calculé, en considérant un coût unitaire de 15 € par mètre cube de terre déplacée.
Correction : Calcul de Volume pour un Talus
1. Calcul de la longueur du talus
Le ratio de pente 3 pour 2 signifie que pour 2 mètres de dénivelé vertical, le talus s’étend sur 3 mètres horizontalement.
Formule :
Pour une hauteur \( h \) donnée, la longueur horizontale \( L \) s’obtient par :
\[ L = \left(\frac{3}{2}\right) \times h \]
Données :
- Hauteur de la coupe : \( h = 12 \) m
Calcul :
\[ L = \left(\frac{3}{2}\right) \times 12 = 18 \text{ m} \]
\bigskip
Résultat :
La longueur horizontale nécessaire pour le talus est de 18 mètres.
2. Calcul du volume du terrassement
Le talus forme un triangle droit dont l’aire de la section transversale est calculée à partir de sa base (longueur horizontale) et de sa hauteur (dénivelé). Ce volume est ensuite obtenu en multipliant l’aire de la section par la longueur totale de la route.
Formules :
- Aire d’un triangle :
\[ A = \frac{1}{2} \times \text{base} \times \text{hauteur} \]
- Volume :
\[ V = A \times \text{Longueur de la route} \]
Données :
- Base du triangle (longueur du talus) : 18 m
- Hauteur du triangle : 12 m
- Longueur totale de la route : 800 m
Calcul :
1. Calcul de l’aire de la section transversale :
\[ A = \frac{1}{2} \times 18 \times 12 \] \[ A = \frac{216}{2} = 108 \text{ m}^2 \]
2. Calcul du volume total :
\[ V = 108 \text{ m}^2 \times 800 \text{ m} \] \[ V = 86\,400 \text{ m}^3 \]
Résultat :
Le volume total de terre à déplacer est de 86 400 m³.
3. Évaluation de la stabilité du talus
La stabilité d’un talus dépend notamment de l’angle du talus comparé à l’angle de frottement interne du sol. Ici, le talus est réalisé avec un ratio de pente de 3 pour 2. Pour obtenir l’angle du talus (\( \theta \)), on utilise la relation trigonométrique :
\[ \tan(\theta) = \frac{\text{vertical}}{\text{horizontal}} \]
Données :
- Dénivelé vertical : 12 m
- Longueur horizontale : 18 m
- Angle de frottement interne du sol : 30°
Calcul :
\[ \tan(\theta) = \frac{12}{18} = 0,6667 \] \[ \Longrightarrow \quad \theta = \arctan(0,6667) \approx 33,7^\circ \]
Conclusion :
L’angle du talus (environ 33,7°) est supérieur à l’angle de frottement interne du sol (30°).
Cela indique que, sans mesures complémentaires (tels que des renforcements ou un terrassement adapté), le talus pourrait être potentiellement instable et nécessiter une attention particulière pour assurer sa sécurité.
4. Estimation des coûts associés au terrassement
Pour estimer le coût total, on multiplie le volume de terre à déplacer par le coût unitaire par mètre cube.
Formule :
\[ \text{Coût total} = \text{Volume} \times \text{Coût unitaire} \]
Données :
- Volume : 86 400 m³
- Coût unitaire : 15 €/m³
Calcul :
\[ \text{Coût total} = 86\,400 \text{ m}^3 \times 15 \,€/ \text{m}^3 \] \[ \text{Coût total} = 1\,296\,000 \,€ \]
Résultat :
L’estimation des coûts pour déplacer le volume de terre est de 1 296 000 €.
Conclusion
- Longueur du talus : 18 m
- Volume de terrassement : 86 400 m³
- Stabilité du talus : Angle de 33,7° (potentiellement instable par rapport à un angle de frottement de 30°)
- Coût estimé : 1 296 000 €
Calcul de Volume pour un Talus
D’autres exercices de terrassement:















0 commentaires