Calcul de l’Isolation Thermique d’un Mur en Bois
Comprendre le Calcul de l’Isolation Thermique d’un Mur en Bois
Vous êtes ingénieur en génie civil et travaillez sur la conception d’un bâtiment résidentiel en bois situé à Grenoble, France. Le bâtiment doit respecter les normes de performance énergétique selon les réglementations européennes.
Pour comprendre le calcul de l’Isolation thermique d’un mur en béton, cliquez sur le lien.
Données:
- Localisation: Grenoble, France
- Zone climatique: Zone H1 (climat montagnard)
- Température extérieure de conception en hiver: -5°C
- Température intérieure souhaitée: 20°C
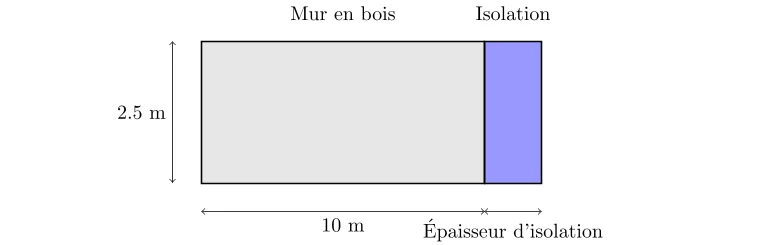
- Dimensions du mur: 10 m de longueur et 2.5 m de hauteur
- Épaisseur du mur en bois: 15 cm
- Conductivité thermique du bois (λ): 0.13 W/m·K
- La résistance thermique requise pour le mur complet, incluant la couche de bois et l’air intérieur/extérieur (en supposant une résistance thermique supplémentaire de \(0.13 \, \text{m}^2\cdot\text{K}/\text{W}\) pour ces couches), est exprimée par l’inégalité suivante : \(R_{\text{total}} \geq 6.67 \, \text{m}^2\cdot\text{K}/\text{W} \) pour répondre à l’exigence de perte de chaleur.
Matériaux disponibles pour l’isolation:
- Laine de verre (λ = 0.032 W/m·K)
- Polystyrène expansé (λ = 0.038 W/m·K)
- Fibre de bois (λ = 0.04 W/m·K)
Question:
Calculer l’épaisseur d’isolation nécessaire pour chaque type de matériau afin d’atteindre une résistance thermique totale (R) qui assure une perte de chaleur ne dépassant pas 0.15 W/m²·K.
Correction : Calcul de l’Isolation Thermique d’un Mur en Bois
Nous devons déterminer l’épaisseur d’isolation à ajouter à un mur en bois afin d’atteindre une résistance thermique totale \( R_{\text{total}} \geq 6,67 \, \text{m}^2\cdot\text{K/W} \) (ce qui correspond à une perte de chaleur ne dépassant pas \( 0,15 \, \text{W/m}^2\cdot\text{K} \)). On nous fournit les caractéristiques du mur et une résistance thermique additionnelle des couches d’air (intérieure/extérieure) de \( 0,13 \, \text{m}^2\cdot\text{K/W} \). L’objectif est de calculer, pour chaque matériau isolant proposé, l’épaisseur nécessaire pour compléter la performance énergétique exigée.
1. Calcul de la résistance thermique du mur en bois (\( R_{\text{bois}} \))
La résistance thermique \( R \) d’un matériau est donnée par la formule
\[ R = \frac{e}{\lambda} \]
où \( e \) est l’épaisseur et \( \lambda \) la conductivité thermique. Ici, le mur en bois lui-même offre une certaine résistance qui contribue à la performance globale.
Formule :
\[ R_{\text{bois}} = \frac{e_{\text{bois}}}{\lambda_{\text{bois}}} \]
Données :
- Épaisseur du mur en bois : \( e_{\text{bois}} = 15 \, \text{cm} = 0,15 \, \text{m} \)
- Conductivité thermique du bois : \( \lambda_{\text{bois}} = 0,13 \, \text{W/m·K} \)
Calcul :
\[ R_{\text{bois}} = \frac{0,15 \, \text{m}}{0,13 \, \text{W/m·K}} \] \[ R_{\text{bois}} \approx 1,1538 \, \text{m}^2\cdot\text{K/W} \]
2. Calcul de la résistance thermique non isolante (\( R_{\text{non iso}} \))
Outre le mur en bois, il existe une résistance thermique fournie par les couches d’air (intérieure et extérieure). Ces deux contributions s’additionnent pour constituer la résistance non isolante.
Données :
- Résistance des couches d’air : \( R_{\text{air}} = 0,13 \, \text{m}^2\cdot\text{K/W} \)
Calcul :
\[ R_{\text{non iso}} = R_{\text{bois}} + R_{\text{air}} \] \[ R_{\text{non iso}} = 1,1538 + 0,13 \] \[ R_{\text{non iso}} \approx 1,2838 \, \text{m}^2\cdot\text{K/W} \]
3. Calcul de la résistance thermique nécessaire de l’isolation (\( R_{\text{iso}} \))
Pour atteindre la performance énergétique requise, la somme de la résistance thermique du mur, des couches d’air et de l’isolation doit être d’au moins \( R_{\text{total}} = 6,67 \, \text{m}^2\cdot\text{K/W} \). La résistance à fournir par l’isolant est donc la différence entre \( R_{\text{total}} \) et \( R_{\text{non iso}} \).
Formule :
\[ R_{\text{iso}} = R_{\text{total}} – R_{\text{non iso}} \]
Données :
- \( R_{\text{total}} = 6,67 \, \text{m}^2\cdot\text{K/W} \)
- \( R_{\text{non iso}} \approx 1,2838 \, \text{m}^2\cdot\text{K/W} \)
Calcul :
\[ R_{\text{iso}} = 6,67 – 1,2838 \] \[ R_{\text{iso}} \approx 5,3862 \, \text{m}^2\cdot\text{K/W} \]
4. Calcul de l’épaisseur d’isolation nécessaire pour chaque matériau
Pour un matériau isolant, la résistance thermique est également donnée par :
\[ R = \frac{e}{\lambda} \quad \Longrightarrow \quad e = R \times \lambda \]
Nous allons calculer \( e \) pour chacun des matériaux :
a) Laine de verre
Données :
- \( \lambda_{\text{Laine de verre}} = 0,032 \, \text{W/m·K} \)
- \( R_{\text{iso}} \approx 5,3862 \, \text{m}^2\cdot\text{K/W} \)
Calcul :
\[ e_{\text{Laine de verre}} = 5,3862 \times 0,032 \] \[ e_{\text{Laine de verre}} \approx 0,1724 \, \text{m} \]
Ce qui correspond à environ 17,24 cm.
b) Polystyrène expansé
Données :
- \( \lambda_{\text{Polystyrène}} = 0,038 \, \text{W/m·K} \)
- \( R_{\text{iso}} \approx 5,3862 \, \text{m}^2\cdot\text{K/W} \)
Calcul :
\[ e_{\text{Polystyrène}} = 5,3862 \times 0,038 \] \[ e_{\text{Polystyrène}} \approx 0,2047 \, \text{m} \]
Ce qui correspond à environ 20,47 cm.
c) Fibre de bois
Données :
- \( \lambda_{\text{Fibre de bois}} = 0,04 \, \text{W/m·K} \)
- \( R_{\text{iso}} \approx 5,3862 \, \text{m}^2\cdot\text{K/W} \)
Calcul :
\[ e_{\text{Fibre de bois}} = 5,3862 \times 0,04 \] \[ e_{\text{Fibre de bois}} \approx 0,2154 \, \text{m} \]
Ce qui correspond à environ 21,54 cm.
Conclusion
Pour que le mur en bois, incluant la résistance des couches d’air, atteigne une résistance thermique totale d’au moins \( 6,67 \, \text{m}^2\cdot\text{K/W} \) (soit une perte de chaleur maximale de \( 0,15 \, \text{W/m}^2\cdot\text{K} \)), il faut ajouter une couche d’isolation ayant :
- Laine de verre : environ 0,1724 m (17,24 cm)
- Polystyrène expansé : environ 0,2047 m (20,47 cm)
- Fibre de bois : environ 0,2154 m (21,54 cm)
Chaque calcul repose sur la relation \( R = \frac{e}{\lambda} \) et prend en compte les résistances déjà existantes dans le mur et les couches d’air. Ces résultats permettent de choisir le matériau isolant et l’épaisseur correspondante pour répondre aux exigences de performance énergétique.
Calcul de l’Isolation Thermique d’un Mur en Bois
D’autres exercices de structure en bois:











0 commentaires