Calcul de la Courbure de la Terre
Comprendre le Calcul de la Courbure de la Terre
En topographie, lorsque l’on réalise un levé sur un terrain étendu, la courbure de la Terre induit une déviation entre la ligne de visée théorique (en ligne droite dans l’espace) et la surface réelle (courbée) de la Terre. Pour obtenir des mesures de dénivelé précises sur de grandes distances, il est nécessaire de corriger les effets de la courbure terrestre. Cet exercice vise à déterminer quantitativement ces corrections.
Données
- Rayon de la Terre : \(\; R = 6\,371\,000 \, \text{m}\)
- Distance horizontale entre deux points (dans le plan tangent) : \(\; d = 5\,000 \, \text{m}\)
- Hauteur d’une station d’observation (pour l’étude de la distance à l’horizon) : \(\; h = 20 \, \text{m}\)
- Pour une deuxième situation (observation réciproque) : Hauteur station A : \(\; h_A = 30 \, \text{m}\), Hauteur station B : \(\; h_B = 10 \, \text{m}\)
Questions
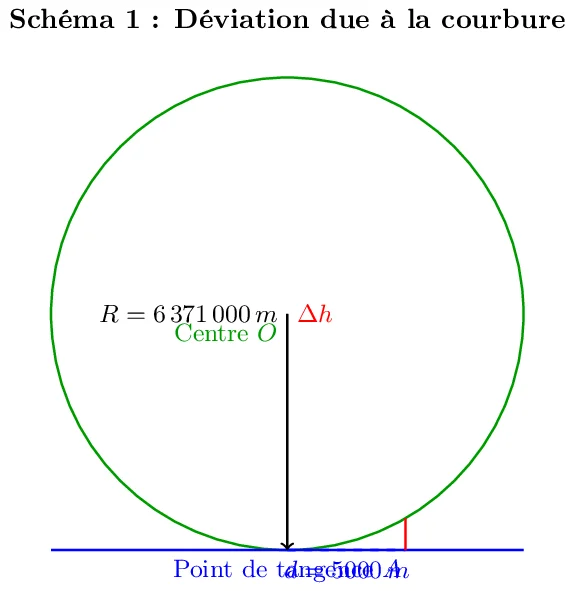
1. Calcul de la déviation due à la courbure sur une distance horizontale :
En considérant que la déviation (ou la « chute ») due à la courbure sur une distance \(d\) est donnée par la formule
\[
\Delta h = \frac{d^2}{2R},
\]
calculez la valeur de \(\Delta h\) pour \( d = 5\,000 \, \text{m} \).
2. Calcul de la distance de visibilité depuis une station d’observation :
La distance à l’horizon depuis un point situé à une hauteur \(h\) au-dessus de la surface de la Terre peut être calculée par la formule
\[
d_h = \sqrt{2 R h + h^2}.
\]
Calculez \( d_h \) pour \( h = 20 \, \text{m} \).
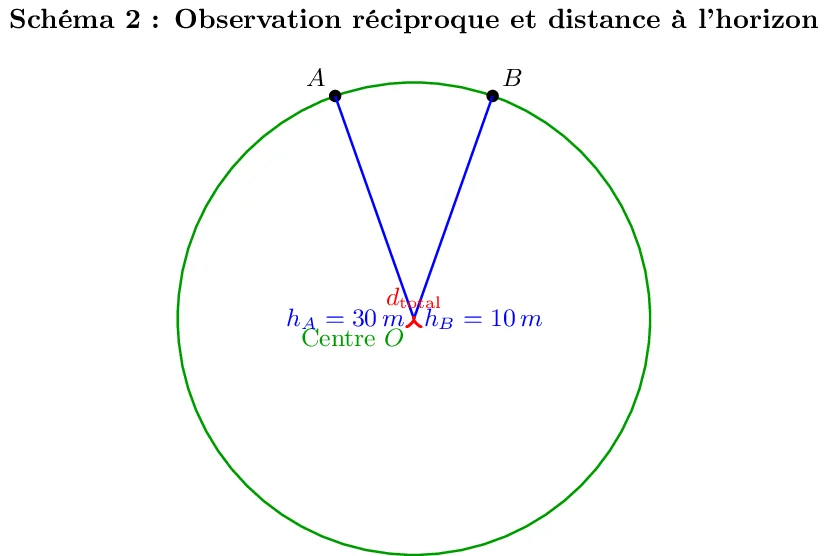
3. Calcul de la distance maximale de visibilité entre deux stations d’observation :
Deux observateurs se trouvent aux hauteurs respectives \(h_A = 30 \, \text{m}\) et \(h_B = 10 \, \text{m}\). La distance maximale à laquelle ces deux stations peuvent se voir l’une l’autre est donnée par la somme des distances à l’horizon pour chacune :
\[
d_{\text{total}} = d_{h_A} + d_{h_B},
\]
avec
\[
d_{h_A} = \sqrt{2 R h_A + h_A^2} \quad \text{et} \quad d_{h_B} = \sqrt{2 R h_B + h_B^2}.
\]
Calculez \( d_{\text{total}} \).
Correction : Calcul de la Courbure de la Terre
1. Calcul de la déviation \( \Delta h \)
Données :
- Distance horizontale : \( d = 5\,000 \, \text{m} \)
- Rayon de la Terre : \( R = 6\,371\,000 \, \text{m} \)
Formule utilisée :
\[ \Delta h = \frac{d^2}{2R} \]
Calcul :
1. Calcul de \( d^2 \)
\[ d^2 = (5\,000)^2 = 25\,000\,000 \, \text{m}^2. \]
2. Calcul de \( 2R \)
\[ 2R = 2 \times 6\,371\,000 \] \[ = 12\,742\,000 \, \text{m}. \]
3. Application de la formule
\[ \Delta h = \frac{25\,000\,000 \, \text{m}^2}{12\,742\,000 \, \text{m}} \] \[ \Delta h \approx 1,961 \, \text{m}. \]
2. Calcul de la distance à l’horizon \( d_h \)
Données :
- Hauteur de la station : \( h = 20 \, \text{m} \)
- Rayon de la Terre : \( R = 6\,371\,000 \, \text{m} \)
Formule utilisée :
\[ d_h = \sqrt{2Rh + h^2} \]
Calcul :
1. Calcul de \( 2Rh \)
\[ 2Rh = 2 \times 6\,371\,000 \times 20 \] \[ = 254\,840\,000 \, \text{m}^2. \]
2. Calcul de \( h^2 \)
\[ h^2 = (20)^2 = 400 \, \text{m}^2. \]
3. Somme des termes
\[ 2Rh + h^2 = 254\,840\,000 + 400 \] \[ = 254\,840\,400 \, \text{m}^2. \]
4. Calcul de la racine carrée
\[ d_h = \sqrt{254\,840\,400} \] \[ d_h \approx 15\,967,5 \, \text{m}. \]
3. Calcul de la distance maximale de visibilité entre deux stations d’observation
a. Calcul de la distance à l’horizon pour chaque station
Données :
- Station A : \( h_A = 30 \, \text{m} \)
- Station B : \( h_B = 10 \, \text{m} \)
- Rayon de la Terre : \( R = 6\,371\,000 \, \text{m} \)
Formule utilisée pour chaque station :
\[ d_{h} = \sqrt{2Rh + h^2} \]
Pour la station A (\( h_A = 30 \, \text{m} \)) :
1. Calcul de \( 2R h_A \)
\[ 2R h_A = 2 \times 6\,371\,000 \times 30 \] \[ = 382\,260\,000 \, \text{m}^2. \]
2. Calcul de \( h_A^2 \)
\[ h_A^2 = (30)^2 = 900 \, \text{m}^2. \]
3. Somme et racine carrée
\[ d_{h_A} = \sqrt{382\,260\,000 + 900} \] \[ d_{h_A} = \sqrt{382\,260\,900} \] \[ d_{h_A} \approx 19\,550,5 \, \text{m}. \]
Pour la station B (\( h_B = 10 \, \text{m} \)) :
1. Calcul de \( 2R h_B \)
\[ 2R h_B = 2 \times 6\,371\,000 \times 10 \] \[ = 127\,420\,000 \, \text{m}^2. \]
2. Calcul de \( h_B^2 \)
\[ h_B^2 = (10)^2 = 100 \, \text{m}^2. \]
3. Somme et racine carrée
\[ d_{h_B} = \sqrt{127\,420\,000 + 100} \] \[ d_{h_B} = \sqrt{127\,420\,100} \] \[ d_{h_B} \approx 11\,292,6 \, \text{m}. \]
b. Calcul de la distance totale de visibilité \( d_{\text{total}} \)
Formule utilisée :
\[ d_{\text{total}} = d_{h_A} + d_{h_B} \]
Substitution des résultats obtenus :
\[ d_{\text{total}} = 19\,550,5 \, \text{m} + 11\,292,6 \, \text{m} \] \[ d_{\text{total}} \approx 30\,843,1 \, \text{m}. \]
Calcul de la Courbure de la Terre
D’autres exercices de topographie:














0 commentaires