Étude des Forces dans les Barres d’une Structure

Comprendre l’Étude des Forces dans les Barres d’une Structure

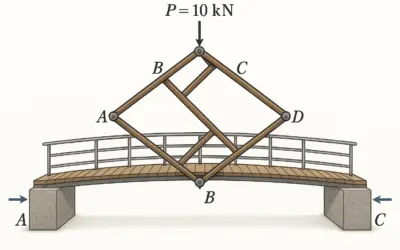
Dans le cadre d’une mission d’ingénierie civile, vous êtes chargé de vérifier la stabilité d’une structure temporaire utilisée lors d’un événement en plein air. La structure est composée de barres d’acier assemblées en forme de tréteau. Vous devez calculer les forces internes dans les barres pour vous assurer qu’elles sont dans les limites de sécurité.

Pour comprendre la Méthode des Nœuds pour un Treillis , cliquez sur le lien.

Données de l’exercice:

La structure est modélisée comme un treillis plan simple.
Les nœuds du treillis sont connectés par des barres en acier dont les propriétés sont homogènes et isotropes.
La structure est soumise à une charge verticale de \(5000 \, \text{N}\) appliquée au sommet du tréteau.
Dimensions de la structure :

– Hauteur du tréteau : \(3 \, \text{m}\)
– Base du tréteau : \(4 \, \text{m}\)

La structure repose sur deux appuis : un appui fixe à l’un des côtés de la base et un appui mobile à l’autre côté.

Note: Les barres ont la même section et le même matériau.

Étude des Forces dans les Barres d’une Structure

Questions:

1. Déterminer les réactions aux appuis en utilisant les conditions d’équilibre.

2. Calculer les forces dans chaque barre du tréteau en appliquant la méthode des nœuds ou la méthode des sections.

Correction : Étude des Forces dans les Barres d’une Structure

1. Calcul des réactions aux appuis

La structure est assimilée à un treillis plan simple, représenté par un triangle dont la base est horizontale (4 m) et la hauteur verticale est de 3 m. La charge verticale de 5000 N est appliquée en son sommet. La structure repose sur deux appuis :

Un appui fixe (A) à l’un des bouts de la base
Un appui mobile (B) à l’autre bout

Pour garantir l’équilibre, nous appliquons les conditions d’équilibre statique :

La somme des forces verticales doit être nulle.
La somme des moments (par exemple autour de A) doit être nulle.

Formules

Somme des forces verticales :

\[ R_{A_y} + R_{B_y} = 5000\,\text{N} \]

Somme des moments autour de A :

\[ R_{B_y} \times L_{AB}\, – 5000\,\text{N} \times d = 0 \]

où \(L_{AB}=4\,\text{m}\) et \(d\) est la distance horizontale entre A et l’application de la charge.

Données

Charge appliquée : 5000 N
Base du treillis : 4 m
Hauteur du treillis : 3 m
Dans un triangle isocèle, le sommet se trouve à mi-distance de la base, donc \(d=2\,\text{m}\).

Calcul

1. Moment autour de A :

\[ R_{B_y} \times 4\,\text{m} = 5000\,\text{N} \times 2\,\text{m} \] \[ R_{B_y} = \frac{10\,000\,\text{N·m}}{4\,\text{m}} \] \[ R_{B_y} = 2500\,\text{N} \]

2. Somme verticale :

\[ R_{A_y} = 5000\,\text{N} – 2500\,\text{N} \] \[ R_{A_y} = 2500\,\text{N} \]

Résultat :

\(R_{A_y}=2500\,\text{N}\)
\(R_{B_y}=2500\,\text{N}\)
La somme des forces horizontales est nulle, donc \(R_{A_x}=0\) (le cas échéant).

2. Calcul des forces dans chaque barre du tréteau par la méthode des sections

a. Géométrie et hypothèses

On considère le triangle défini par :

Point A : (0, 0)
Point B : (4, 0)
Point C (sommet où s’applique la charge) : (2, 3)

Les barres du treillis sont :

Barre AC reliant A à C
Barre BC reliant B à C
Barre AB reliant A à B (la traverse inférieure)

b. Calculs géométriques

Pour la barre AC (même raisonnement pour BC) :

Différence horizontale : \(\Delta x = 2\,\text{m}\)
Différence verticale : \(\Delta y = 3\,\text{m}\)

Longueur de la barre :

\[ L_{AC} = \sqrt{(2)^2 + (3)^2} \] \[ L_{AC} = \sqrt{4+9} \] \[ L_{AC} = \sqrt{13}\,\text{m} \]

Angles :

\[ \sin\theta = \frac{3}{\sqrt{13}}, \quad \cos\theta = \frac{2}{\sqrt{13}} \]

c. Méthode d’équilibre au nœud C

Au nœud C, la charge de 5000 N s’exerce verticalement vers le bas. Les deux barres AC et BC contribuent à compenser cette charge. En considérant la symétrie et en posant :

\(F_{AC}\) : force dans la barre AC
\(F_{BC}\) : force dans la barre BC

Équilibre horizontal au nœud C :

La composante horizontale de \(F_{AC}\) est dirigée vers l’intérieur (vers A) et celle de \(F_{BC}\) vers l’intérieur (vers B) :

\[ F_{AC}\cos\theta = F_{BC}\cos\theta \] \[ \Rightarrow \quad F_{AC}=F_{BC} \]

Équilibre vertical au nœud C :

Les composantes verticales des deux forces doivent compenser la charge :

\[ F_{AC}\sin\theta + F_{BC}\sin\theta = 5000\,\text{N} \]

Comme \(F_{AC}=F_{BC}\), on obtient :

\[ 2F_{AC}\sin\theta = 5000\,\text{N} \] \[ \Rightarrow \quad F_{AC} = \frac{5000}{2\sin\theta} \]

En remplaçant \(\sin\theta\) :

\[ F_{AC} = \frac{5000}{2 \times \frac{3}{\sqrt{13}}} = \frac{5000\sqrt{13}}{6} \]

Calcul numérique :

\[ \sqrt{13} \approx 3,606 \]

\[ \Rightarrow \quad F_{AC} \approx \frac{5000 \times 3,606}{6} \] \[ F_{AC} \approx \frac{18\,030}{6} \] \[ F_{AC} \approx 3005\,\text{N} \]

Résultat pour les barres inclinées :

\(F_{AC} \approx 3005\,\text{N}\) (traction)
\(F_{BC} \approx 3005\,\text{N}\) (traction)

d. Calcul de la force dans la barre horizontale AB

Pour trouver la force dans la barre AB, on peut faire l’équilibre au nœud A.

Au nœud A :

La réaction verticale est de 2500\,N (vers le haut).
La barre AC exerce une force \(F_{AC} \approx 3005\,\text{N}\) dirigée vers C.

Sa composante verticale :

\[ F_{AC,y} = 3005 \times \sin\theta \] \[ F_{AC,y} \approx 3005 \times \frac{3}{3,606} \] \[ F_{AC,y} \approx 3005 \times 0,832 \] \[ F_{AC,y} \approx 2500\,\text{N} \]

Sa composante horizontale :

\[ F_{AC,x} = 3005 \times \cos\theta \] \[ F_{AC,x} \approx 3005 \times \frac{2}{3,606} \] \[ F_{AC,x} \approx 3005 \times 0,555 \] \[ F_{AC,x} \approx 1669\,\text{N} \]

À l’appui A, pour assurer l’équilibre horizontal, la barre AB doit compenser cette composante horizontale.
Ainsi :

\[ F_{AB} \approx 1669\,\text{N} \]

La direction est opposée à celle de la composante de AC, indiquant une compression dans la barre AB.

Synthèse des résultats

1. Réactions aux appuis :

\(R_{A_y} = 2500\,\text{N}\)
\(R_{B_y} = 2500\,\text{N}\)
\(R_{A_x} = 0\,\text{N}\) (aucune force horizontale externe)

2. Forces dans les barres (méthode des sections) :

Barre AC : \(F_{AC} \approx 3005\,\text{N}\) en traction
Barre BC : \(F_{BC} \approx 3005\,\text{N}\) en traction
Barre AB : \(F_{AB} \approx 1669\,\text{N}\) en compression

Étude des Forces dans les Barres d’une Structure

D’autres exercices de Rdm:

Étude des Forces dans les Barres d’une Structure