Calcul du Centre de Gravité d’une Poutre
Comprendre le Calcul du Centre de Gravité d’une Poutre
Dans le cadre de la conception d’une structure métallique légère pour une nouvelle installation sportive, un ingénieur doit déterminer le centre de gravité d’une poutre en acier composée de différentes sections hétérogènes pour assurer une stabilité optimale. La poutre est composée de trois sections rectangulaires avec des densités de matériaux différents.
Pour comprendre le calcul de Contrainte et Raccourcissement dans une Poutre, cliquez sur le lien.
Données fournies:
- Dimensions et matériaux des sections:
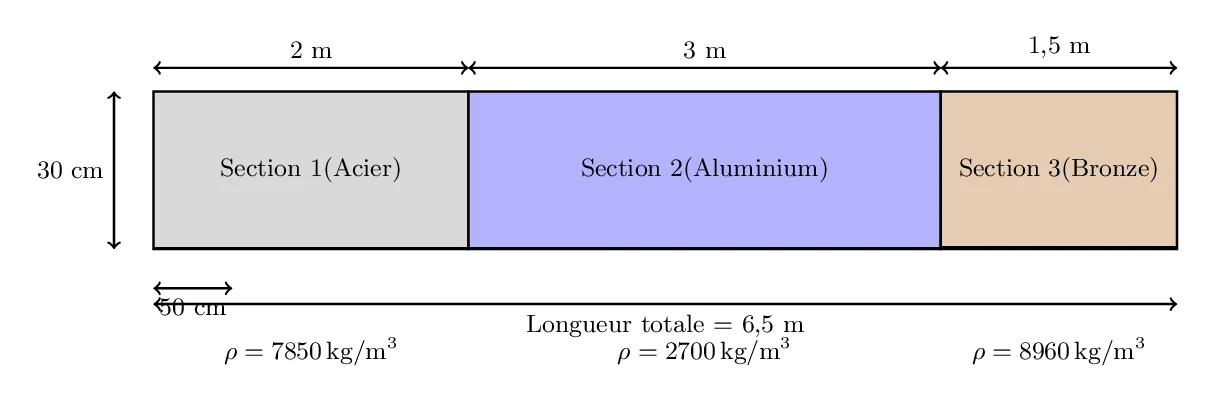
- Section 1: Longueur = 2 m, largeur = 50 cm, hauteur = 30 cm, densité = 7,850 kg/m³ (acier).
- Section 2: Longueur = 3 m, largeur = 50 cm, hauteur = 30 cm, densité = 2,700 kg/m³ (aluminium).
- Section 3: Longueur = 1.5 m, largeur = 50 cm, hauteur = 30 cm, densité = 8,960 kg/m³ (bronze).
Question:
Calculer le centre de gravité de la poutre composite en considérant que les sections sont disposées bout à bout dans l’ordre donné (acier, aluminium, bronze), alignées le long de l’axe horizontal.
Correction : Calcul du Centre de Gravité d’une Poutre
1. Calcul des masses de chaque section
Donnée :
Chaque section a la même aire de la section transversale :
\[ A = \text{largeur} \times \text{hauteur} \] \[ A = 0{,}50\,\text{m} \times 0{,}30\,\text{m} \] \[ A = 0{,}15\,\text{m}^2 \]
Formule :
\[ \text{Masse } (m) = \text{densité } (\rho) \times \text{volume } (V) \] où \[V = L \times A \]
a) Section 1 (Acier)
Données :
\(L_1 = 2\,\text{m}\), \(\rho_1 = 7850\,\text{kg/m}^3\)
- Calcul du volume :
\[ V_1 = 2\,\text{m} \times 0{,}15\,\text{m}^2 \] \[ V_1 = 0{,}30\,\text{m}^3 \]
- Calcul de la masse :
\[ m_1 = 7850\,\text{kg/m}^3 \times 0{,}30\,\text{m}^3 \] \[ m_1 = 2355\,\text{kg} \]
b) Section 2 (Aluminium)
Données :
\(L_2 = 3\,\text{m}\), \(\rho_2 = 2700\,\text{kg/m}^3\)
- Calcul du volume :
\[ V_2 = 3\,\text{m} \times 0{,}15\,\text{m}^2 \] \[ V_2 = 0{,}45\,\text{m}^3 \]
- Calcul de la masse :
\[ m_2 = 2700\,\text{kg/m}^3 \times 0{,}45\,\text{m}^3 \] \[ m_2 = 1215\,\text{kg} \]
c) Section 3 (Bronze)
Données :
\(L_3 = 1{,}5\,\text{m}\), \(\rho_3 = 8960\,\text{kg/m}^3\)
- Calcul du volume :
\[ V_3 = 1{,}5\,\text{m} \times 0{,}15\,\text{m}^2 \] \[ V_3 = 0{,}225\,\text{m}^3 \]
- Calcul de la masse :
\[ m_3 = 8960\,\text{kg/m}^3 \times 0{,}225\,\text{m}^3 \] \[ m_3 = 2016\,\text{kg} \]
2. Détermination des positions des centres de gravité de chaque section
On suppose que l’origine (\(x=0\)) est à l’extrémité gauche de la poutre. Pour une section homogène, le CG se trouve au milieu de sa longueur.
a) Section 1 (Acier)
- Position :
S’étendant de \(x=0\) à \(x=2\,\text{m}\), le centre est :
\[ x_1 = \frac{2}{2} = 1\,\text{m} \]
b) Section 2 (Aluminium)
- Position :
Cette section débute à \(x=2\,\text{m}\) et se termine à \(x=5\,\text{m}\). Son centre est donc :
\[ x_2 = 2\,\text{m} + \frac{3}{2} \] \[ x_2 = 2 + 1{,}5 \] \[ x_2 = 3{,}5\,\text{m} \]
c) Section 3 (Bronze)
- Position :
Elle commence à \(x=5\,\text{m}\) et se termine à \(x=6{,}5\,\text{m}\). Son centre est :
\[ x_3 = 5\,\text{m} + \frac{1{,}5}{2} \] \[ x_3 = 5 + 0{,}75 \] \[ x_3 = 5{,}75\,\text{m} \]
3. Calcul du centre de gravité de la poutre composite
Formule générale :
\[ x_{CG} = \frac{\sum_{i=1}^{3} m_i\,x_i}{\sum_{i=1}^{3} m_i} \]
Substitution des valeurs :
- Moment de la Section 1 :
\[ m_1\,x_1 = 2355\,\text{kg} \times 1\,\text{m} \] \[ m_1\,x_1 = 2355\,\text{kg·m} \]
- Moment de la Section 2 :
\[ m_2\,x_2 = 1215\,\text{kg} \times 3{,}5\,\text{m} \] \[ m_2\,x_2 = 4252{,}5\,\text{kg·m} \]
- Moment de la Section 3 :
\[ m_3\,x_3 = 2016\,\text{kg} \times 5{,}75\,\text{m} \] \[ m_3\,x_3 = 11592\,\text{kg·m} \]
Somme des moments :
\[ \sum m_i\,x_i = 2355 + 4252{,}5 + 11592 \] \[ \sum m_i\,x_i = 18199{,}5\,\text{kg·m} \]
Somme des masses :
\[ \sum m_i = 2355 + 1215 + 2016 \] \[ \sum m_i = 5586\,\text{kg} \]
Calcul final :
\[ x_{CG} = \frac{18199{,}5}{5586} \approx 3{,}26\,\text{m} \]
Conclusion
Le centre de gravité de la poutre composite se situe à environ 3,26 m de l’extrémité gauche de la poutre
Calcul du Centre de Gravité d’une Poutre
D’autres exercices de Rdm:















0 commentaires