Calculs de Géométrie et de Drainage vrd
Comprendre les Calculs de Géométrie et de Drainage vrd
La ville de Pluviaville envisage de construire une nouvelle route pour améliorer l’accès à une nouvelle zone résidentielle en développement. La route doit être conçue pour assurer une gestion efficace des eaux pluviales, en évitant les accumulations d’eau qui pourraient affecter à la fois la route elle-même et les zones résidentielles adjacentes.
Pour comprendre le Calcul des Capacités des Canalisations, cliquez sur le lien.
Données fournies:
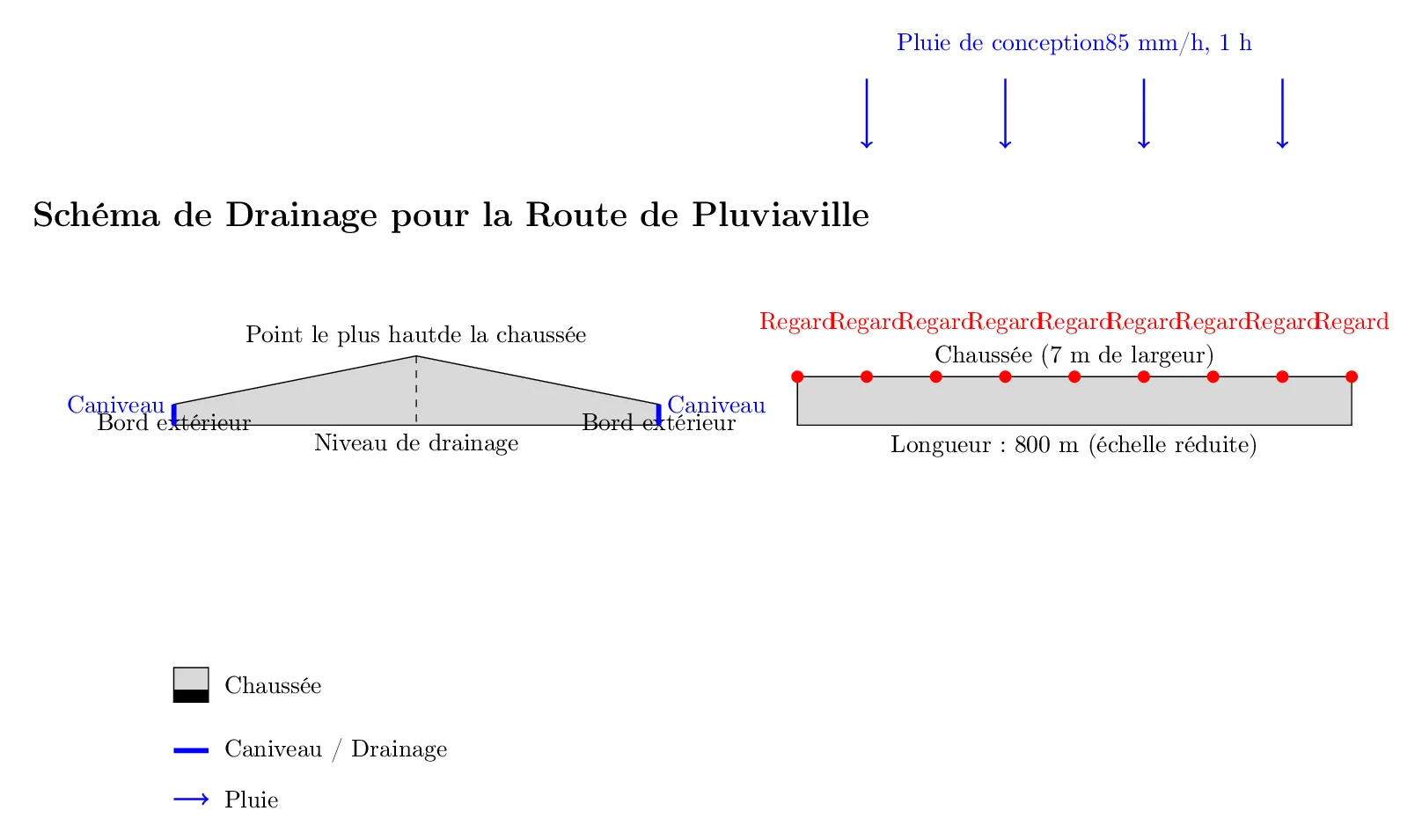
- Longueur de la route: 800 mètres.
- Largeur de la chaussée: 7 mètres.
- Pente transversale de la chaussée: 2% (la chaussée doit incliner de 2% de son centre vers les côtés pour favoriser l’écoulement des eaux).
- Intensité de la pluie de conception: 85 mm/h (correspond à une pluie ayant une période de retour de 10 ans pour cette région).
- Durée de la pluie de conception: 1 heure.
- Coefficient de ruissellement: 0.9 pour la surface asphaltée.
Questions:
1. Calcul de la quantité d’eau à gérer:
- Calculer le volume total d’eau qui ruissellera sur la surface de la route pendant la durée de la pluie de conception.
2. Conception du système de drainage:
- Déterminer le nombre et le placement des caniveaux et regards nécessaires le long de la route.
- Choisir un diamètre approprié pour les conduites de drainage qui transporteront l’eau vers le système de gestion des eaux pluviales le plus proche.
Correction : Calculs de Géométrie et de Drainage vrd
1. Calcul de la quantité d’eau à gérer
Étape 1 : Détermination de la surface de la route
Donnée :
- Longueur \(L = 800\) m
- Largeur \(W = 7\) m
Calcul :
\[ \text{Surface} \; A = L \times W \] \[ \text{Surface} \; A = 800 \times 7 \] \[ \text{Surface} \; A = 5600 \; \text{m}^2 \]
Étape 2 : Conversion de l’intensité de la pluie
Donnée :
- Intensité de pluie = 85 mm/h
- Durée de la pluie = 1 h
Conversion :
\[ \text{Hauteur de pluie} \; h = 85 \; \text{mm} = 0,085 \; \text{m} \]
Étape 3 : Calcul du volume de pluie théorique sur la route
Formule :
\[ V_{\text{théorique}} = A \times h \]
Calcul :
\[ V_{\text{théorique}} = 5600 \; \text{m}^2 \times 0,085 \; \text{m} = 476 \; \text{m}^3 \]
Étape 4 : Application du coefficient de ruissellement
Donnée :
- Coefficient de ruissellement \(C = 0,9\) (pour une surface asphaltée)
Formule :
\[ V_{\text{effectif}} = V_{\text{théorique}} \times C \]
Calcul :
\[ V_{\text{effectif}} = 476 \; \text{m}^3 \times 0,9 \] \[ V_{\text{effectif}} = 428,4 \; \text{m}^3 \]
Conclusion 1 :
La quantité totale d’eau à gérer pendant la durée de la pluie est de 428,4 m³.
2. Conception du système de drainage
Étape 1 : Détermination du débit de conception
Pour évacuer le volume total en 1 heure, le débit moyen nécessaire est :
Formule :
\[ Q = \frac{V_{\text{effectif}}}{\text{Durée}} \]
Calcul :
\[ Q = \frac{428,4 \; \text{m}^3}{3600 \; \text{s}} \approx 0,119 \; \text{m}^3/\text{s} \]
Conclusion 2.1 :
Le système de drainage doit être capable d’évacuer un débit d’environ 0,12 m³/s.
Étape 2 : Choix du diamètre de la conduite de drainage
On utilisera la formule de Manning pour dimensionner une conduite circulaire pleine :
Formule de Manning :
\[ Q = \frac{1}{n} \cdot A \cdot R^{2/3} \cdot S^{1/2} \]
avec :
- \(n\) : coefficient de Manning (pour du béton, \(n \approx 0,013\))
- \(A\) : aire de la section
- \(R\) : rayon hydraulique
- \(S\) : pente hydraulique
Pour une conduite circulaire pleine de diamètre \(D\) :
- Aire
\[ A = \frac{\pi D^2}{4} \]
- Rayon hydraulique
\[ R = \frac{D}{4} \] (car \(R = \frac{A}{P}\) et le périmètre mouillé \(P = \pi D\) pour un cercle complet)
On suppose ici que la pente hydraulique est équivalente à la pente transversale donnée, soit \(S = 0,02\).
Calcul détaillé
1. Substitution des expressions dans la formule de Manning :
\[ Q = \frac{1}{n} \cdot \frac{\pi D^2}{4} \cdot \left(\frac{D}{4}\right)^{2/3} \cdot S^{1/2} \]
2. Mise en forme avec les valeurs numériques :
- \(n = 0,013\) donc \(\frac{1}{n} \approx 76,92\)
- \(\frac{\pi}{4} \approx 0,7854\)
- \(\left(\frac{D}{4}\right)^{2/3} = \frac{D^{2/3}}{4^{2/3}}\) avec \(4^{2/3} \approx 2,52\)
- \(S^{1/2} = \sqrt{0,02} \approx 0,1414\)
Ainsi, la formule devient :
\[ Q \approx 76,92 \times 0,7854 \times \frac{D^{2 + 2/3}}{2,52} \times 0,1414 \]
Notons que \(D^2 \times D^{2/3} = D^{8/3}\).
3. Calcul des constantes :
- \(76,92 \times 0,7854 \approx 60,43\)
- \(60,43 / 2,52 \approx 23,99\)
- Puis, \(23,99 \times 0,1414 \approx 3,3936\)
On obtient donc :
\[ Q \approx 3,3936 \times D^{8/3} \]
4. Recherche du diamètre \(D\) :
On impose \(Q = 0,119 \; \text{m}^3/\text{s}\) :
\[ 0,119 = 3,3936 \times D^{8/3} \]
D’où :
\[ D^{8/3} = \frac{0,119}{3,3936} \approx 0,03504 \]
Pour isoler \(D\), on élève les deux côtés à la puissance \(3/8\) :
\[ D = \left(0,03504\right)^{\frac{3}{8}} \]
5. Calcul final :
\[ \ln(0,03504) \approx -3,350 \] \[ \Rightarrow \quad \left(0,03504\right)^{0,375} = \exp(0,375 \times -3,350) \] \[ \approx \exp(-1,256) \approx 0,285 \; \text{m} \]
Arrondi : On retient un diamètre standard de 300 mm.
Conclusion 2.2 :
Le diamètre recommandé pour la conduite de drainage est d’environ 0,3 m (300 mm).
Étape 3 : Nombre et placement des caniveaux et regards
La conception du réseau de collecte doit permettre une évacuation efficace de l’eau. Voici une proposition basée sur des pratiques courantes :
-
Collecte :
La chaussée est conçue avec une pente transversale de 2 % pour faciliter l’écoulement de l’eau vers les bords.
→ Installation de caniveaux sur chacun des côtés de la route. -
Placement des regards :
Pour permettre le raccordement, l’inspection et la maintenance du système, on peut prévoir des regards à intervalles réguliers.Hypothèse de conception :
- Espacement d’environ 100 m le long de la route.
- Pour une route de 800 m, cela conduit à l’installation d’un regard tous les 100 m, soit environ 9 regards (en comptant les extrémités).
Conclusion 2.3 :
- Caniveaux : Installer un caniveau de chaque côté de la route pour recueillir l’eau ruisselante.
- Regards : Prévoir des regards tous les 100 m, ce qui correspond à environ 9 regards sur l’ensemble de la route.
Calculs de Géométrie et de Drainage vrd
D’autres exercices de Vrd:














0 commentaires